例1 画出函数y=3sin(2x+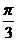 ),x∈R的简图
),x∈R的简图
解:(五点法)由T=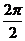 ,得T=π 列表:
,得T=π 列表:
|
x |
– |
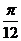 |
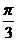 |
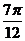 |
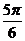 |
2x+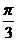 |
0 |
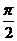 |
π |
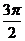 |
2π |
3sin(2x+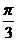 |
0 |
3 |
0 |
–3 |
0 |
描点画图:

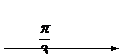 这种曲线也可由图象变换得到:
这种曲线也可由图象变换得到:
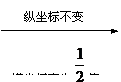
即:y=sinx
y=sin(x+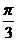 )
)

y=sin(2x+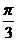 ) y=3sin(2x+
) y=3sin(2x+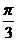 )
)
一般地,函数y=Asin(ωx+ ),x∈R(其中A>0,ω>0)的图象,可以看作用下面的方法得到:
),x∈R(其中A>0,ω>0)的图象,可以看作用下面的方法得到:
先把正弦曲线上所有的点向左(当 >0时)或向右(当
>0时)或向右(当 <0时=平行移动|
<0时=平行移动| |个单位长度,再把所得各点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的
|个单位长度,再把所得各点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的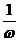 倍(纵坐标不变),再把所得各点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)
倍(纵坐标不变),再把所得各点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)
另外,注意一些物理量的概念:
A :称为振幅;T=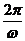 :称为周期;f=
:称为周期;f=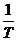 :称为频率;
:称为频率;
ωx+ :称为相位
:称为相位 x=0时的相位
x=0时的相位 称为初相
称为初相
评述:由y=sinx的图象变换出y=sin(ωx+ )的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换
)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换
途径一:先平移变换再周期变换(伸缩变换)
先将y=sinx的图象向左( >0)或向右(
>0)或向右( <0=平移|
<0=平移| |个单位,再将图象上各点的横坐标变为原来的
|个单位,再将图象上各点的横坐标变为原来的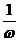 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+ )的图象
)的图象
途径二:先周期变换(伸缩变换)再平移变换
先将y=sinx的图象上各点的横坐标变为原来的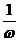 倍(ω>0),再沿x轴向左(
倍(ω>0),再沿x轴向左( >0)或向右(
>0)或向右( <0=平移
<0=平移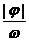 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+ )的图象
)的图象
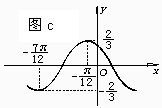
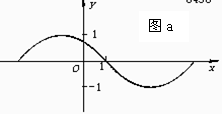
例2已知如图是函数y=2sin(ωx+ )其中|
)其中| |<
|<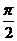 的图象,那么
的图象,那么
 A
A ω=
ω=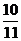 ,
, =
= B
B ω=
ω=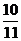 ,
, =-
=-
C ω=2,
ω=2, =
= D
D ω=2,
ω=2, =-
=-
解析:由图可知,点(0,1)和点(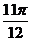 ,0)都是图象上的点
,0)都是图象上的点 将点(0,1)的坐标代入待定的函数式中,得2sin
将点(0,1)的坐标代入待定的函数式中,得2sin =1,即sin
=1,即sin =
=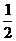 ,又|
,又| |<
|<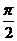 ,∴
,∴ =
=
又由“五点法”作图可知,点(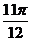 ,0)是“第五点”,所以ωx+
,0)是“第五点”,所以ωx+ =2π,即ω·
=2π,即ω·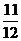 π+
π+ =2π,解之得ω=2,故选C
=2π,解之得ω=2,故选C
解此题时,若能充分利用图象与函数式之间的联系,则也可用排除法来巧妙求解,即:
解:观察各选择答案可知,应有ω>0
观察图象可看出,应有T=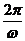 <2π,∴ω>1 ,故可排除A与B
<2π,∴ω>1 ,故可排除A与B
由图象还可看出,函数y=2sin(ωx+ )的图象是由函数y=2sinωx的图象向左移而得到的
∴
)的图象是由函数y=2sinωx的图象向左移而得到的
∴ >0,又可排除D,故选C
>0,又可排除D,故选C
例3已知函数y=Asin(ωx+ ),在同一周期内,当x=
),在同一周期内,当x=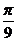 时函数取得最大值2,当x=
时函数取得最大值2,当x=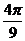 时函数取得最小值-2,则该函数的解析式为( )
时函数取得最小值-2,则该函数的解析式为( )
A y=2sin(3x-
y=2sin(3x- )
B
)
B y=2sin(3x+
y=2sin(3x+ )
)
C y=2sin(
y=2sin(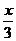 +
+ )
D
)
D y=2sin(
y=2sin(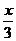 -
- )
)
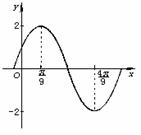 解析:由题设可知,所求函数的图象如图所示,点(
解析:由题设可知,所求函数的图象如图所示,点(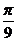 ,2)和点(
,2)和点(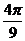 ,-2)都是图象上的点,且由“五点法”作图可知,这两点分别是“第二点”和“第四点”,所以应有:
,-2)都是图象上的点,且由“五点法”作图可知,这两点分别是“第二点”和“第四点”,所以应有:
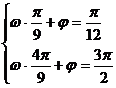 解得
解得 答案:B
答案:B
由y=Asin(ωx+ )的图象求其函数式:
)的图象求其函数式:
一般来说,在这类由图象求函数式的问题中,如对所求函数式中的A、ω、 不加限制(如A、ω的正负,角
不加限制(如A、ω的正负,角 的范围等),那么所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所致),因此这类问题多以选择题的形式出现,我们解这类题的方法往往因题而异,但逆用“五点法”作图的思想却渗透在各不同解法之中
的范围等),那么所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所致),因此这类问题多以选择题的形式出现,我们解这类题的方法往往因题而异,但逆用“五点法”作图的思想却渗透在各不同解法之中
|
16.(本小题13分) (1) 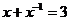 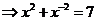 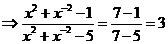 (2)解析:设F(x)=f(x)-2,即F(x)=alog2x+blog3x, 则F()=alog2+blog3=-(alog2x+blog3x)=-F(x), ∴F(2010)=-F()=-[f()-2]=-2, 即f(2010)-2=-2,故f(2010)=0 |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
17.(本小题13分) A={x|-1<x≤5}. (1) 当m=3时,B={x|-1<x<3}, 则∁RB={x|x≤-1或x≥3}, ∴A∩(∁RB)={x|3≤x≤5}. (2)∵A={x|-1<x≤5},A∩B={x|-1<x<4}, ∴有-42+2×4+m=0,解得m=8, 此时B={x|-2<x<4},符合题意. |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效
|
18.(本小题13分) (1)证明:∵f(x+2)=-f(x), ∴f(x+4)=-f(x+2)=-[-f(x)]=f(x), ∴f(x)是以4为周期的周期函数. (2)当0≤x≤1时,f(x)=x, 设-1≤x≤0,则0≤-x≤1, ∴f(-x)=(-x)=-x.∵f(x)是奇函数, ∴f(-x)=-f(x),∴-f(x)=-x, 即f(x)=x.故f(x)=x(-1≤x≤1) 又设1<x<3,则-1<x-2<1, ∴f(x-2)=(x-2), 又∵f(x-2)=-f(2-x)=-f[(-x)+2] =-[-f(-x)]=-f(x), ∴-f(x)=(x-2), ∴f(x)=-(x-2)(1<x<3). ∴f(x)= 由f(x)=-,解得x=-1.∵f(x)是以4为周期的周期函数.故f(x)=-的所有x=4n-1(n∈Z).令0≤4n-1≤2010,则≤n≤502,又∵n∈Z,∴1≤n≤502(n∈Z),∴在[0,2010]上共有502个x使f(x)=-. |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
19.(本小题13分) (1)由已知得,函数的定义域为 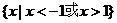 , ,关于原点对称; 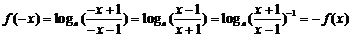 故  是偶函数。 是偶函数。(2)当 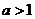 时,在定义域 时,在定义域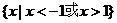 内,函数 内,函数 与函数 与函数 的单调性一致; 的单调性一致; , ,易得, 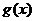 分别在区间 分别在区间 内为单调递减。 内为单调递减。所以,函数  区间 区间 内为单调递减; 内为单调递减;(3)由已知得 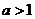 ,由(2)可知,函数 ,由(2)可知,函数 在 在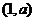 内单调递减,所以有 内单调递减,所以有 即 即 即  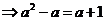 xsc解之得 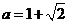 (负值舍去) (负值舍去) |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
20.(本小题14分) (1)当甲的用水量不超过6吨时,即  时,乙的用水量也不会超过6吨,此时 时,乙的用水量也不会超过6吨,此时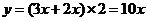 ; ;当甲的用水量超过6吨而乙的用水量没有超过6吨时,即 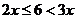 时,此时 时,此时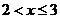 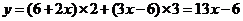 当甲乙的用水量都超过6吨时,即 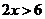 时, 时,此时 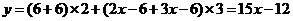 综上可知, 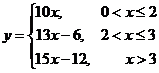 (2)若 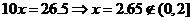 (舍去) (舍去)若 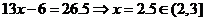 (符合题意) (符合题意)若 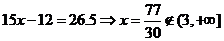 (舍去) (舍去)综上可知,甲的用水量为  (吨) (吨)付费 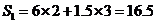 (元) (元)乙的用水量为  (吨) (吨)付费 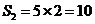 (元) (元)答:略。 |

 请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
21.(本小题7+7=14分) (1) 法一:特殊点法 在直线 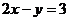 上任取两点(2、1)和(3、3),……1分 上任取两点(2、1)和(3、3),……1分则 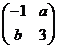 · · 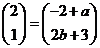 即得点 即得点 …3 分 …3 分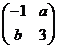 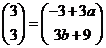 即得点 即得点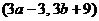 将 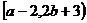 和 和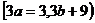 分别代入 分别代入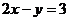 上得 上得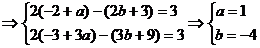 则矩阵 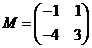 则 则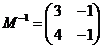 法二:通法 设  为直线 为直线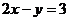 上任意一点其在M的作用下变为 上任意一点其在M的作用下变为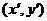 则 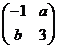 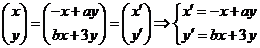 代入 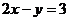 得: 得: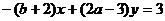 其与 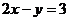 完全一样得 完全一样得 则矩阵 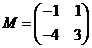 则 则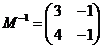 (2) 解:(Ⅰ)消去参数 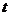 ,得直线 ,得直线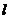 的普通方程为 的普通方程为 …3分 …3分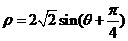 ,即 ,即 , ,两边同乘以  得 得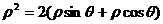 , ,得⊙ 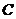 的直角坐标方程为 的直角坐标方程为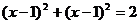 ………5分 ………5分(Ⅱ)圆心 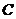 到直线 到直线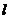 的距离 的距离 ,所以直线 ,所以直线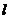 和⊙ 和⊙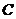 相交…7分 相交…7分(3).解:由 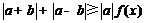 ,且 ,且 , ,得 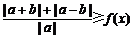 ……3分 ……3分又因为 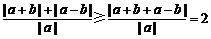 ,则有2 ,则有2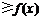 ………5分 ………5分解不等式  ,得 ,得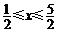 …………………… 7分 …………………… 7分 |
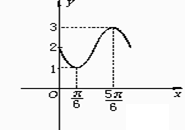 C
C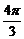 ,φ=-
,φ=-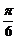
 B
B
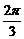 ,φ=-
,φ=- D
D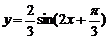 B
B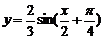
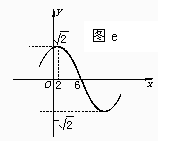 C
C D
D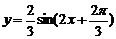
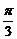 时,有ymax=2,当x=0时,有ymin=-2?,则函数表达式是
时,有ymax=2,当x=0时,有ymin=-2?,则函数表达式是 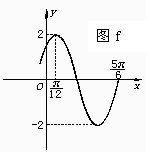 5
5 的一段图象,则函数f(x)的表达式为
的一段图象,则函数f(x)的表达式为 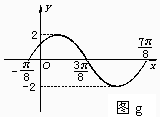 8
8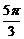 时,y有最大值为
时,y有最大值为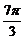 ,当x=
,当x=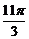 时,y有最小值-
时,y有最小值-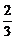 ,求此函数的解析式
,求此函数的解析式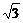 cos(x-θ)为偶函数,求θ的值
cos(x-θ)为偶函数,求θ的值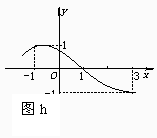 由图g所示函数图象,求y=Asin(ωx+φ)
由图g所示函数图象,求y=Asin(ωx+φ)

 ),由这个最高点到相邻最低点的图象与x轴交于点(6,0),试求函数的解析式
),由这个最高点到相邻最低点的图象与x轴交于点(6,0),试求函数的解析式 =
=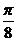
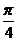 +
+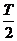 ,由此可求ω的值,再将最高(或低)点坐标代入可求
,由此可求ω的值,再将最高(或低)点坐标代入可求 倍
倍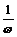 倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图
倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图