17.解:(Ⅰ)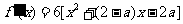
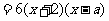 .
………………… 3分
.
………………… 3分
当 时,
时,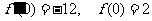 ,
,
所以切线方程为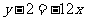 ,即
,即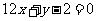 .
………………… 6分
.
………………… 6分
(Ⅱ)令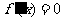 ,解得:
,解得: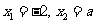 .
.
① 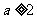 ,则当
,则当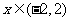 时,
时,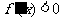 ,函数
,函数 在
在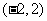 上单调递减,
上单调递减,
所以,当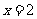 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为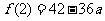 . ………………… 8分
. ………………… 8分
② 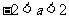 ,则当
,则当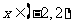 时,
时,
当 变化时,
变化时,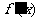 ,
, 的变化情况如下表:
的变化情况如下表:
 |
 |
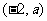 |
 |
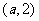 |
 |
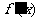 |
|
 |
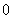 |
 |
|
 |
 |
 |
极小值 |
 |
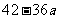 |
所以,当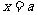 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为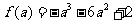 .………………… 11分
.………………… 11分
③  ,则当
,则当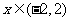 时,
时,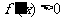 ,函数
,函数 在
在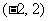 上单调递增,
上单调递增,
所以,当 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为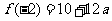 . ………………… 13分
. ………………… 13分
综上,当 时,
时, 的最小值为
的最小值为 ;当
;当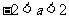 时,
时, 的最小值为
的最小值为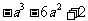 ;当
;当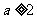 时,
时, 的最小值为
的最小值为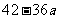 .
………………… 14分
.
………………… 14分

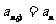 ,所以
,所以 ,解得
,解得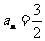 或
或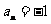 (舍去).
(舍去). 的任意性知,
的任意性知, .
………………… 3分
.
………………… 3分 ,则
,则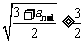 ,得
,得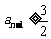 ,
, ,…,
,…,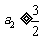 ,
,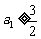 ,与
,与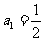 矛盾.
矛盾.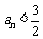 .
………………… 8分
.
………………… 8分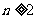 时,
时,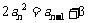 ,
,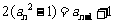 ,
,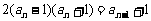 ,
,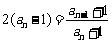 .
.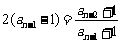 ,…,
,…,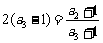 ,
,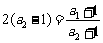 .
. 个式子相乘,得
个式子相乘,得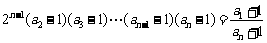 ,
,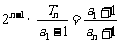 ,
,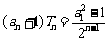 .
.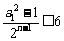 对任意
对任意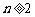 恒成立.
恒成立.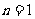 时,
时,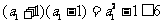 ,
,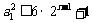 对任意
对任意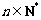 恒成立.
恒成立.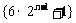 单调递增,所以
单调递增,所以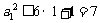 ,
,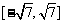 .
………………… 14分
.
………………… 14分
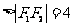 ,
, 是以
是以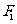 ,
,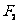 为焦点,长轴长为
为焦点,长轴长为 的椭圆,其方程为
的椭圆,其方程为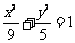 . ………………… 5分
. ………………… 5分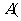
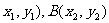 ,由条件可知
,由条件可知 为
为 的中点,
的中点, ………………… 9分
………………… 9分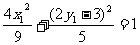 ,整理为
,整理为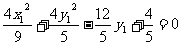 .
.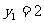 ,再代入椭圆方程解得
,再代入椭圆方程解得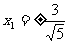 ,
,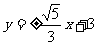 .
………………… 13分
.
………………… 13分 的斜率存在,设其方程为
的斜率存在,设其方程为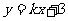 .
.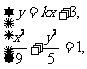 得
得 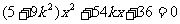 . 令
. 令 ,解得
,解得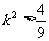 .
.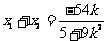 , ①
, ① 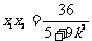 . ②
………… 8分
. ②
………… 8分 ,所以
,所以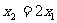 .
.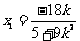 ,
,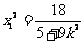 ,
,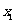 得
得 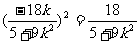 ,
………………… 11分
,
………………… 11分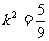 ,
,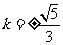 .
. ,则点
,则点 的个数共有
的个数共有 个,列举如下:
个,列举如下: ,
,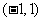 ,
,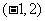 ,
,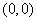 ,
,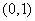 ,
,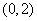 ,
,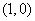 ,
,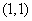 ,
,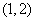 ,
,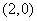 ,
,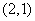 ,
,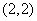 .
.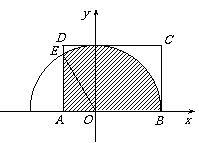 故点
故点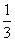 . …………………
5分
. …………………
5分 ,则区域
,则区域 的面积是
的面积是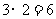 .
. 的点
的点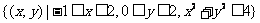 ,即图中的阴影部分.
………………… 9分
,即图中的阴影部分.
………………… 9分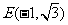 ,
,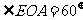 ,
,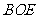 的面积是
的面积是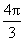 ,
,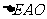 的面积是
的面积是 ,
,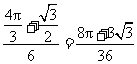 .
………………… 13分
.
………………… 13分
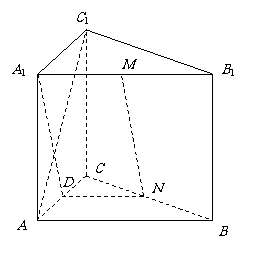
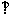 平面
平面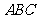 ,
,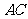 是
是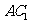 在平面
在平面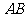
 .
………………… 6分
.
………………… 6分 平面
平面 ,即
,即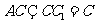 ,
, .
………………… 4分
.
………………… 4分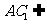 平面
平面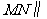 平面
平面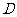 ,
, ,
,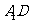 .
. 分别是
分别是 的中点,
的中点,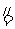
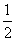
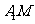 =
= ,
,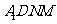 是平行四边形.
是平行四边形.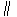
 .
………………… 11分
.
………………… 11分 平面
平面 平面
平面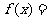
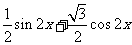 ………………… 3分
………………… 3分 2
………………… 5分
2
………………… 5分
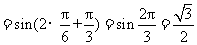 .
………………… 7分
.
………………… 7分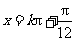 (
(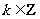 )时,
)时, .
………………… 9分
.
………………… 9分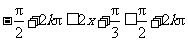 ,
,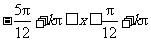 ,
,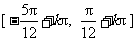 ,
,
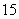 11.
11.
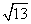 12.
12.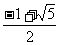 13.
13.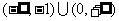 14.
14.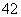
 满足
满足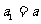 ,
,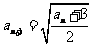 ,
,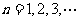 .
.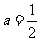 时,证明:
时,证明: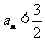 ;
;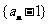 的前
的前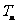 .若对任意正整数
.若对任意正整数 成立,求
成立,求