14、(湖北省八校2009届高三第二次联考文)在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答对这道题的概率是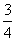 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是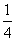 .
.
(Ⅰ)求乙、丙两人各自回答对这道题的概率.
(Ⅱ)求甲、乙、丙三人中恰有两人回答对该题的概率.
 解:
解: 记“甲回答对这道题”、“ 乙回答对这道题”、“丙回答对这道题”分别为事件
记“甲回答对这道题”、“ 乙回答对这道题”、“丙回答对这道题”分别为事件 、
、 、
、 ,则
,则 ,且有
,且有 ,即
,即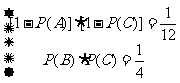
∴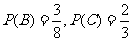
(2)由(1)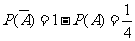 ,
, .
.
则甲、乙、丙三人中恰有两人回答对该题的概率为:

15(09江西高二其中)某科技公司遇到一个技术难题,紧急成立甲、乙两个攻关小组,按
要求各自单独进行为期一个月的技术攻关,同时决定对攻关期满就攻克技术难题的小组给予奖励.已知此技术难题在攻关期满时被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为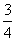 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设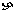 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递减”为事件
在定义域内单调递减”为事件 ,求事件
,求事件 的概率.
的概率.
解:记“甲攻关小组获奖”为事件A,则 ,记“乙攻关小组获奖”为事件B,则
,记“乙攻关小组获奖”为事件B,则 .
.
(1)由题意,ξ的所有可能取值为0,1,2.
 ,
,
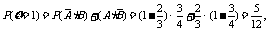
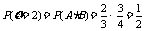 ,
,
∴ξ的分布列为:
|
ξ |
0 |
1 |
2 |
|
P |
 |
 |
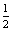 |
∴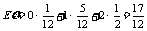 .
.
(2)∵获奖攻关小组数的可能取值为0,1,2,相对应没有获奖的攻关小组的取值为2,1,0.∴η的可能取值为0,4.
当η=0时, 在定义域内是增函数.
在定义域内是增函数.
当η=4时, 在定义域内是减函数.
在定义域内是减函数.
∴ .
.
9月份更新


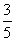
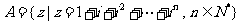 ,
, ,(
,(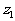 可以等于
可以等于 ),从集合
),从集合 中任取一元素,则该元素的模为
中任取一元素,则该元素的模为 的概率为______________。
的概率为______________。
 中任取一个元素,所取元素
中任取一个元素,所取元素 的概率是
的概率是 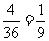 ;
; .
.  ;
; .
. .
.  、
、 两项技术
两项技术 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.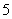 个零件进行检测,求其中至多
个零件进行检测,求其中至多 个零件是合格品的概率;
个零件是合格品的概率; 个,设
个,设 表示其中合格品的个数,求
表示其中合格品的个数,求 与
与 .
. 、
、 .
. ,
, .
.
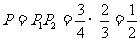 .
.
 .
.
 ,
, ,
,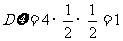 .
.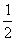 ,因此
,因此 =
=
 ,向上的点数是偶数出现的次
,向上的点数是偶数出现的次 ,可得:当
,可得:当
 或
或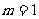 ,
, 时,
时, 当
当 ,
, 或
或 因此
因此






