摘要:∴当t=时取得最小值.最小值为2+3.即k≤2+3. ∴k的取值范围为(-∞.2+3]
网址:http://m.1010jiajiao.com/timu_id_94579[举报]
如图,某小区准备绿化一块直径为 的半圆形空地,
的半圆形空地, 外的地方种草,
外的地方种草, 的内接正方形
的内接正方形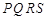 为一水池,其余地方种花.若
为一水池,其余地方种花.若
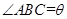 ,设
,设 的面积为
的面积为 ,正方形
,正方形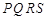 的面积为
的面积为 ,将比值
,将比值 称为“规划合理度”.
称为“规划合理度”.
(1)试用 ,
, 表示
表示 和
和 .
.
(2)当 为定值,
为定值, 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角 的大小.
的大小.

【解析】第一问中利用在
 ABC中
ABC中  ,
,
 =
= 设正方形的边长为
设正方形的边长为 则
则 
 然后解得
然后解得
第二问中,利用 而
而 =
=
借助于  为减函数
得到结论。
为减函数
得到结论。
(1)、 如图,在
 ABC中
ABC中  ,
,
 =
=
设正方形的边长为 则
则 

 =
=

(2)、 而
而 =
= ∵0 <
∵0 <  <
<
 ,又0 <2
,又0 <2 <
< ,
, 0<t£1
0<t£1
 为减函数
为减函数
当 时
时  取得最小值为
取得最小值为 此时
此时
查看习题详情和答案>>
设三次函数![]() 在x=1处取得极值,其图象在x=m处的切线的斜率为-3a.
在x=1处取得极值,其图象在x=m处的切线的斜率为-3a.
(1)求证:![]() ;
;
(2)若函数y=f(x)在区间[s,t]上单调递增,求![]() 的取值范围;
的取值范围;
(3)问是否存在实数k(k是与a,b,c,d无关的常数),当x≥k时,恒有![]() 恒成立?若存在,试求出k的最小值;若不存在,请说明理由.
恒成立?若存在,试求出k的最小值;若不存在,请说明理由.
设三次函数f(x)=ax3+bx2+cx+d(a<b<c),在x=1处取得极值,其图像在x=m处的切线的斜率为-3a.
(1)求证:![]() ;
;
(2)若函数y=f(x)在区间[s,t]上单调递增,求|s-t|的取值范围;
(3)问是否存在实数k(k是与a,b,c,d无关的常数),当x≥k时,恒有![]() 恒成立?若存在,试求出k的最小值;若不存在,请说明理由.
恒成立?若存在,试求出k的最小值;若不存在,请说明理由.