题目内容
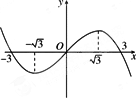
设三次函数f(x)＝ax3＋bx2＋cx＋d(a＜b＜c)，在x＝1处取得极值，其图像在x＝m处的切线的斜率为－3a．
(1)求证：
；
(2)若函数y＝f(x)在区间[s，t]上单调递增，求|s－t|的取值范围；
(3)问是否存在实数k(k是与a，b，c，d无关的常数)，当x≥k时，恒有
恒成立？若存在，试求出k的最小值；若不存在，请说明理由．
答案：
解析：
解析：
(1)
，由题设，得
①
②
∵
由①代入②得
得
③
将
代入
中，得
④
由③、④得
；…………5分
(1)由(1)知，
∴方程
的判别式有两个不等实根
，
又，∴
∴当
或
时，
，当
时，
∴函数
的单调区间是
，∴
，
由知
．
∵函数在区间[s，t]上单调递增，∴[s，t]
，
∴
，即
的取值范围是
，…………10分
(2)由
，即
∵
，令
，
要使
在
上恒成立，
只需
即
，∴
或
由题意，得
∴存在实数k满足条件，即k的最小值为
．…………14分
练习册系列答案
金钥匙试卷系列答案
相关题目
(x)，函数y＝x·
)，极小值为f(－
是函数y＝f(x)的导数y＝
的导数，若方程
＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．”
，则它的对称中心为________；
＝________．
；
恒成立？若存在，试求出k的最小值；若不存在，请说明理由．