摘要:[解答](I)由题意及正弦定理.得.
网址:http://m.1010jiajiao.com/timu_id_94438[举报]
设数列 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在 ,使得
,使得 成立,则称数列
成立,则称数列 为“Jk型”数列.
为“Jk型”数列.
(1)若数列 是“J2型”数列,且
是“J2型”数列,且 ,
, ,求
,求 ;
;
(2)若数列 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列 是等比数列.
是等比数列.
【解析】1)中由题意,得 ,
, ,
, ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,
所以.
(2)中证明:由{ }是“j4型”数列,得
}是“j4型”数列,得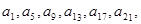 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{ }是“j3型”数列,得
}是“j3型”数列,得
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
查看习题详情和答案>>
已知函数 (
( 为实数).
为实数).
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)若 在
在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
【解析】第一问中由题意可知: . ∵
. ∵ ∴
∴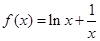 ∴
∴
 .
.
当 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
第二问
 .
.
当 时,
时, ,在
,在 上有
上有 ,
, 递增,符合题意;
递增,符合题意;
令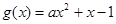 ,则
,则
 ,∴
,∴ 或
或 在
在 上恒成立.转化后解决最值即可。
上恒成立.转化后解决最值即可。
解:(Ⅰ) 由题意可知: . ∵
. ∵ ∴
∴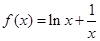 ∴
∴
 .
.
当 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
(Ⅱ) 
 .
.
当 时,
时, ,在
,在 上有
上有 ,
, 递增,符合题意;
递增,符合题意;
令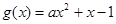 ,则
,则
 ,∴
,∴ 或
或 在
在 上恒成立.∵二次函数
上恒成立.∵二次函数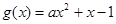 的对称轴为
的对称轴为 ,且
,且
∴ 或
或
 或
或
 或
或
 或
或 . 综上
. 综上
查看习题详情和答案>>
若函数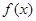 在定义域内存在区间
在定义域内存在区间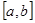 ,满足
,满足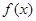 在
在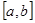 上的值域为
上的值域为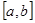 ,则称这样的函数
,则称这样的函数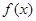 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数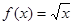 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出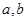 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数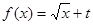 为“优美函数”,求实数
为“优美函数”,求实数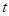 的取值范围.
的取值范围.
【解析】第一问中,利用定义,判定由题意得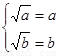 ,由
,由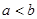 ,所以
,所以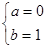
第二问中, 由题意得方程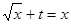 有两实根
有两实根
设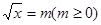 所以关于m的方程
所以关于m的方程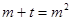 在
在 有两实根,
有两实根,
即函数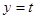 与函数
与函数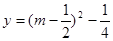 的图像在
的图像在 上有两个不同交点,从而得到t的范围。
上有两个不同交点,从而得到t的范围。
解(I)由题意得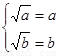 ,由
,由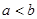 ,所以
,所以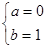 (6分)
(6分)
(II)由题意得方程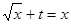 有两实根
有两实根
设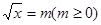 所以关于m的方程
所以关于m的方程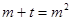 在
在 有两实根,
有两实根,
即函数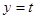 与函数
与函数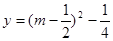 的图像在
的图像在 上有两个不同交点。
上有两个不同交点。
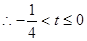
查看习题详情和答案>>
 在
在 取得极值
取得极值 的单调区间(用
的单调区间(用 表示);
表示); ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求

 在
在
 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

 由(1)知:
由(1)知:  ,
,

 ,
,




 …..3分
…..3分
 , 使
, 使


 得:
得: 
 中,内角
中,内角 的对边的边长分别为
的对边的边长分别为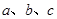 ,且
,且
 的大小;
的大小; 求
求 的最小值.
的最小值.
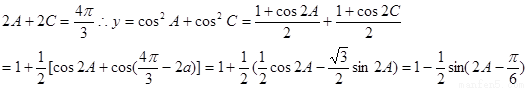

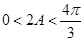 ,
, ,则当
,则当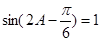 ,即
,即 时,y的最小值为
时,y的最小值为 .
.