摘要:又当时.存在..对所有的满足条件.
网址:http://m.1010jiajiao.com/timu_id_92568[举报]
(本小题满分14分) 已知函数![]() 及正整数数列
及正整数数列![]() . 若
. 若![]() ,且当
,且当![]() 时,有
时,有![]() ; 又
; 又![]() ,
,![]() ,且
,且![]() 对任意
对任意![]() 恒成立. 数列
恒成立. 数列![]() 满足:
满足:![]() .
.
(1) 求数列![]() 及
及![]() 的通项公式;
的通项公式;
(2) 求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3) 证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
(本小题满分12分)奇函数![]() ,且当
,且当![]() 时,
时,![]() 有最小值
有最小值![]() ,又
,又![]() .(1)求
.(1)求![]() 的表达式;
的表达式;
(2)设![]() ,正数数列
,正数数列![]() 中,
中,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,数列
,数列![]() 中
中![]() ,
,![]() .是否存在常数
.是否存在常数![]() 使
使![]() 对任意
对任意![]() 恒成立.若存在,求
恒成立.若存在,求![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
 ; 又
; 又 对任意
对任意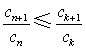 对任意
对任意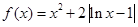 .
.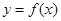 的最小值;
的最小值; 恒成立;
恒成立;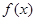 图象上的不同两点
图象上的不同两点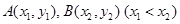 ,如果在函数
,如果在函数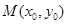 (其中
(其中 )使得点
)使得点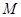 处的切线
处的切线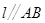 ,则称直线
,则称直线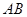 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当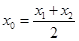 时,又称直线
时,又称直线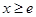 时,对于函数
时,对于函数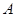 、
、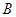 ,直线
,直线