摘要：(1)分别求出≤40和≥40时与之间的关系式,
网址：http://m.1010jiajiao.com/timu_id_8331[举报]
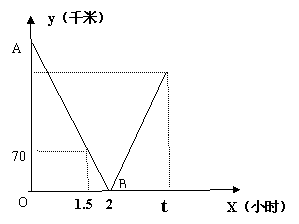
两辆校车分别从甲、乙两站出发，匀速相向而行,相遇后继续前行，已知两车相遇时中巴比大巴多行驶40千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至中巴到达乙站这一过程中y与x之间的函数关系. 根据图象提供的信息，解答下列问题：
（1）请你说明点B、点C的实际意义;
(2) 求线段AB所在直线的函数关系式和甲、乙两站的距离；
（3）求两车速度及中巴从甲站到乙站所需的时间t；
（4）若中巴到达乙站后立刻返回甲站，大巴到达甲站后停止行驶，请你在图中补全这一过程中y关于x的函数的大致图象.
 |
查看习题详情和答案>>
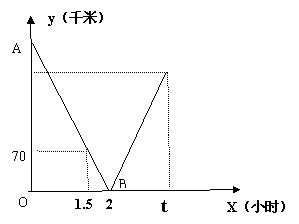
两辆校车分别从甲、乙两站出发，匀速相向而行,相遇后继续前行，已知两车相遇时中巴比大巴多行驶40千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至中巴到达乙站这一过程中y与x之间的函数关系. 根据图象提供的信息，解答下列问题：
（1）请你说明点B、点C的实际意义;
(2) 求线段AB所在直线的函数关系式和甲、乙两站的距离；
（3）求两车速度及中巴从甲站到乙站所需的时间t；
（4）若中巴到达乙站后立刻返回甲站，大巴到达甲站后停止行驶，请你在图中补全这一过程中y关于x的函数的大致图象.
 |
查看习题详情和答案>>
A县和B县春季分别急需化肥100吨和60吨，C县和D县分别储存化肥110吨和50吨，全部调配给A县和B县．运费如下表所示：
（1）设从C县运到A县的化肥为x吨，则从C县运往B县的化肥为
（2）求总运费W（元）与x（吨）之间的函数关系式，并写出自变量x的取值范围；
（3）求最低总运费，并说明运费最低时的运送方案．
查看习题详情和答案>>
| 出发地 运费（元/吨） 目的地 |
C县 |
D县 |
| A县 | 40 | 45 |
| B县 | 35 | 50 |
（110-x）
（110-x）
吨，从D县运往A县的化肥为（100-x）
（100-x）
吨，从D县运往B县的化肥为（x-50）
（x-50）
吨；（2）求总运费W（元）与x（吨）之间的函数关系式，并写出自变量x的取值范围；
（3）求最低总运费，并说明运费最低时的运送方案．
(千克)与生长时间
(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克，在第40天后每天的需水量比前一天增加100千克.