摘要：∵l2与x轴的交点A,顶点坐标是,l1与l2关于x轴对称. ∴l2过A,顶点坐标是(0.4)-----------1分 ∴y=ax2+4---------2分 ∴0=4a+4 得 a=-1 ∴l2的解析式为y=-x2+4------------3分 (2)设B(x1 ,y1) ∵点B在l1上 ∴B(x1 ,x12-4) ----------------4分 ∵四边形ABCD是平行四边形.A.C关于O对称 ∴B.D关于O对称 ∴D(-x1 ,-x12+4).---------------6分 将D(-x1 ,-x12+4)的坐标代入l2:y=-x2+4 ∴左边=右边 ∴点D在l2上.-------------7分 (3)设平行四边形ABCD的面积为S,则 S=2*S△ABC =AC*|y1|=4|y1| a.当点B在x轴上方时.y1＞0 ∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大. ∴S既无最大值也无最小值----------8分 b.当点B在x轴下方时.-4≤y1＜0 ∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小. ∴当y1 =-4时.S由最大值16.但他没有最小值 此时B在y轴上.它的对称点D也在y轴上.9分 ∴AC⊥BD ∴平行四边形ABCD是菱形----------10分
网址：http://m.1010jiajiao.com/timu_id_8114[举报]
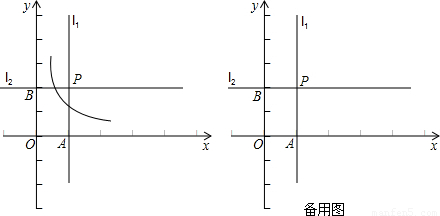
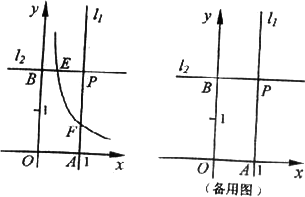
在平面直角坐标系XOY中，直线l1过点A（1，0）且与y轴平行，直线l2过点B（0，2）且与x轴平行，直线l1与直线l2相交于点P，点E为直线l2上一点，反比例函数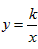
（k＞0）的图象过点E与直线l1相交于点F。
（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF，若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由。
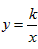（k＞0）的图象过点E与直线l1相交于点F。（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF，若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由。
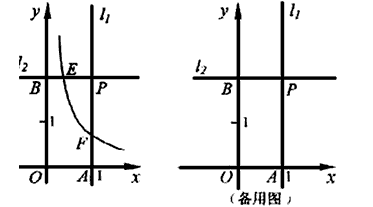
在平面直角坐标系XOY中，直线l1过点A（1，0）且与y轴平行，直线l2过点B（0，2）且与x轴平行，直线l1与直线l2相交于点P．点E为直线l2上一点，反比例函数
（k＞0）的图象过点E与直线l1相交于点F．
（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF．若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由．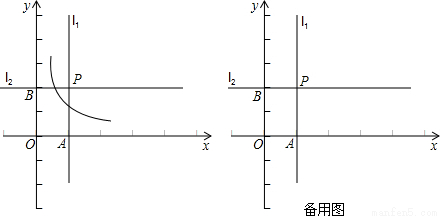
查看习题详情和答案>>
（k＞0）的图象过点E与直线l1相交于点F．（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF．若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由．
查看习题详情和答案>>
在平面直角坐标系XOY中，直线l1过点A（1，0）且与y轴平行，直线l2过点B（0，2）且与x轴平行，直线l1与直线l2相交于点P．点E为直线l2上一点，反比例函数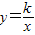
（k＞0）的图象过点E与直线l1相交于点F．
（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF．若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由．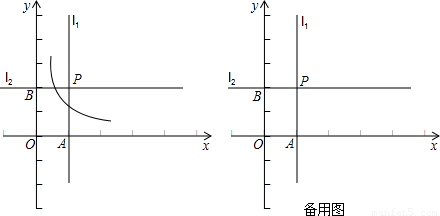
查看习题详情和答案>>
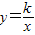（k＞0）的图象过点E与直线l1相交于点F．（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF．若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由．
查看习题详情和答案>>
（k＞0）的图象过点E与直线l1相交于点F．
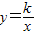(k＞0)的图象过点E与直线l1相交于点F．