摘要:整理.得解得..
网址:http://m.1010jiajiao.com/timu_id_7991[举报]
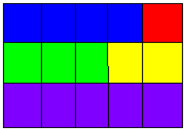 17、如图,是一张“3×5”(表示边长分别为3和5)的长方形,现要把它分成若干张边长为整数的长方形(包括正方形)纸片,并要求分得的任何两张纸片都不完全相同.
17、如图,是一张“3×5”(表示边长分别为3和5)的长方形,现要把它分成若干张边长为整数的长方形(包括正方形)纸片,并要求分得的任何两张纸片都不完全相同.(1)能否分成5张满足上述条件的纸片?解:能,
(2)能否分成6张满足上述条件的纸片?解:不能,因为要剪成六张完全不同的纸片需要(1+2+3+4+5+6)=21个方格,而3*5=15 15<21,所以不能.
(若能分,用“a×b”的形式分别表示出各张纸片的边长,并画出分割的示意图;若不能分,请说明理由.)
先阅读,再解答问题.
例:解不等式
>1
解:把不等式
>1进行整理,得
-1>0,即
>0.
则有(1)
或(2)
.
解不等式组(1)得
<x<1,解不等式组(2)知其无解,所以得不等式的解为
<x<1.
请根据以上解不等式的思想方法解不等式
<2.
查看习题详情和答案>>
例:解不等式
| x |
| 2x-1 |
解:把不等式
| x |
| 2x-1 |
| x |
| 2x-1 |
| 1-x |
| 2x-1 |
则有(1)
|
|
解不等式组(1)得
| 1 |
| 2 |
| 1 |
| 2 |
请根据以上解不等式的思想方法解不等式
| 3x+2 |
| x-2 |
先阅读,后解答:解方程组
解:由①式得y=9-x ③
把③式代入②式,得
5x+3(9-x)=33
整理,得x=3 ④
把④式代入③式,得y=6x=3
∴y=6
请用以上方法解方程组:
.
查看习题详情和答案>>
|
解:由①式得y=9-x ③
把③式代入②式,得
5x+3(9-x)=33
整理,得x=3 ④
把④式代入③式,得y=6x=3
∴y=6
请用以上方法解方程组:
|
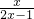 >1
>1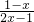 >0.
>0.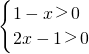 或(2)
或(2)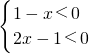 .
. <x<1,解不等式组(2)知其无解,所以得不等式的解为
<x<1,解不等式组(2)知其无解,所以得不等式的解为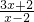 <2.
<2.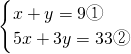
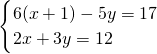 .
.