摘要:记l2=g(t)=-[t-2(x0-3)]2+4(x0-1)2.若x0>3,则2(x0-3) (0, 4x0-8),所以当t=2(x0-3),即=2(x0-3)时,l有最大值2(x0-1).若2<x0<3,则2(x0-3)0,g(t)在区间(0.4 x0-8)上是减函数.所以0<l2<16(x0-2),l不存在最大值.综上所述.当x0>3时.点P(x0,0)的“相关弦 的弦长中存在最大值.且最大值为2(x0-1),当2< x03时.点P(x0,0)的“相关弦 的弦长中不存在最大值.
网址:http://m.1010jiajiao.com/timu_id_78600[举报]
、设函数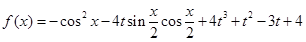 ,
,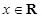 ,其中|t|≤1,将f(x)的最小值记为g(t).
,其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤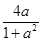 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
查看习题详情和答案>>
设函数![]() ,
,![]() ,
,
其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤![]() 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
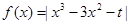
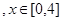 的最大值记为g(t),当t在实数范围内变化时g(t)最小值为
的最大值记为g(t),当t在实数范围内变化时g(t)最小值为