摘要:如图.在以点为圆心.为直径的半圆中..是半圆弧上一点..曲线是满足为定值的动点的轨迹.且曲线过点.(Ⅰ)建立适当的平面直角坐标系.求曲线的方程,(Ⅱ)设过点的直线l与曲线相交于不同的两点..若△的面积不小于.求直线斜率的取值范围.解:本小题主要考查直线.圆和双曲线等平面解析几何的基础知识.考查轨迹方程的求法.不等式的解法以及综合解题能力.(Ⅰ)解法1:以O为原点.AB.OD所在直线分别为x轴.y轴.建立平面直角坐标系.则A,P().依题意得
网址:http://m.1010jiajiao.com/timu_id_78254[举报]
(本小题满分13分)
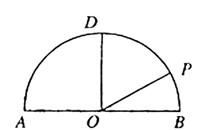
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,
∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P。
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F。若△OEF的面积不小于2![]() ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。
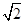 ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。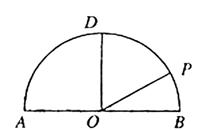
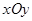 中,以
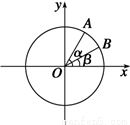
中,以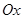 轴为始边作两个锐角
轴为始边作两个锐角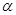 ,
,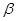 ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于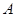 ,
,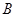 两点,已知
两点,已知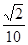 ,
,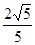 .
.
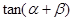 的值;
的值; 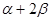 的值.
的值.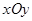 中,以
中,以 轴为始边作两个锐角
轴为始边作两个锐角 ,
, ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于 ,
,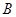 两点,已知
两点,已知 ,
, .
.
 的值;
的值;  的值.
的值.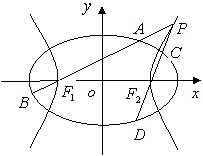 (Ⅰ)求椭圆和双曲线的标准方程;
(Ⅰ)求椭圆和双曲线的标准方程;