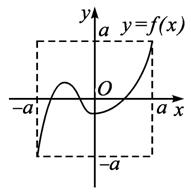摘要： 函数的定义域为A. B. C. D. 解:函数的定义域必须满足条件:
网址：http://m.1010jiajiao.com/timu_id_78236[举报]
定义域为R的函数f（x）满足条件：
①[f(x1)-f(x2)](x1-x2)＞0，(x1，x2∈R+，x1≠x2)；
②f（x）+f（-x）=0（x∈R）；
③f（-3）=0．
则不等式x•f（x）＜0的解集是（ ）
①[f(x1)-f(x2)](x1-x2)＞0，(x1，x2∈R+，x1≠x2)；
②f（x）+f（-x）=0（x∈R）；
③f（-3）=0．
则不等式x•f（x）＜0的解集是（ ）
查看习题详情和答案>>
定义域为R的函数f（x）满足条件：
①
；
②f（x）+f（-x）=0（x∈R）；
③f（-3）=0．
则不等式x•f（x）＜0的解集是（ ）
A．{x|-3＜x＜0或x＞3}
B．{x|x＜-3或0≤x＜3}
C．{x|x＜-3或x＞3}
D．{x|-3＜x＜0或0＜x＜3}
查看习题详情和答案>>
①
；②f（x）+f（-x）=0（x∈R）；
③f（-3）=0．
则不等式x•f（x）＜0的解集是（ ）
A．{x|-3＜x＜0或x＞3}
B．{x|x＜-3或0≤x＜3}
C．{x|x＜-3或x＞3}
D．{x|-3＜x＜0或0＜x＜3}
查看习题详情和答案>>
定义域为R的函数f(x)满足：
①[f(x1)－f(x2)](x1＜x2)＞0，(x1，x2∈R+，x1≠x2)；
②f(x)＋f(－x)＝0(x∈R)；
③f(－3)＝0．
则不等式x·f(x)＜0的解集是
[ ]
A．
{x|－3＜x＜0或x＞3}
B．
{x|x＜－3或0≤x＜3}
C．
{x|x＜－3或x＞3}
D．
{x|－3＜x＜0或0＜x＜3}
定义域和值域均为[-a，a]（常数a＞0）的函数y=f（x）和y=g（x）的图象如图所示：
