题目内容
定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,给出下列四个命题: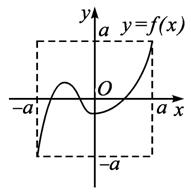

①方程f[g(x)]=0有且仅有三个解;
②方程g[f(x)]=0有且仅有三个解;
③方程f[f(x)]=0有且仅有九个解;
④方程g[g(x)]=0有且仅有一个解.
那么,其中的正确命题是( )
A.①③ B.②③ C.③④ D.①④
解析:由图知f(x)的图象与x轴有3个交点,g(x)的图象与x轴有且仅有一个交点,设f(x)=0的三个根分别为x1、x2、x3。则x1、x2、x3∈[-a,a],再设g(x)=0的一个根为x4,x4∈[-a,a].
则由f(g(x))=0![]() g(x)=x1或g(x)=x2或g(x)=x3,再由g(x)的单调性知f[g(x)]=0有且仅有三个解,因此①是正确的,同理可判断②,③皆错,④对,因此答案应为D.
g(x)=x1或g(x)=x2或g(x)=x3,再由g(x)的单调性知f[g(x)]=0有且仅有三个解,因此①是正确的,同理可判断②,③皆错,④对,因此答案应为D.
答案:D

练习册系列答案
相关题目
若函数f(x)=log2
的定义域和值域均为[1,+∞),则实数a的取值集合为( )
| x2+ax+1 |
| x |
| A、{0} |
| B、{a|0≤a≤1} |
| C、{a|a≥0} |
| D、{a|a≥2} |
