题目内容
定义域为R的函数f(x)满足条件:
①[f(x1)-f(x2)](x1-x2)>0,(x1,x2∈R+,x1≠x2);
②f(x)+f(-x)=0(x∈R);
③f(-3)=0.
则不等式x•f(x)<0的解集是( )
①[f(x1)-f(x2)](x1-x2)>0,(x1,x2∈R+,x1≠x2);
②f(x)+f(-x)=0(x∈R);
③f(-3)=0.
则不等式x•f(x)<0的解集是( )
分析:由条件①可得函数f(x)为(0,+∞)上的增函数,由②可得函数为奇函数,再由③可得函数的图象过
点(-3,0)、(3,0),数形结合可得不等式的解集
点(-3,0)、(3,0),数形结合可得不等式的解集
解答: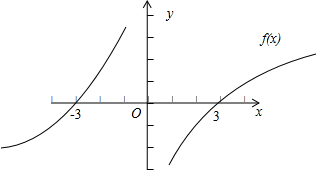 解:由条件①可得函数f(x)为(0,+∞)
解:由条件①可得函数f(x)为(0,+∞)
上的增函数,
由②可得函数为奇函数,
再由③可得函数的图象过点(-3,0)、(3,0),
故由不等式x•f(x)<0可得,
当x>0时,f(x)<0;
当x<0时,f(x)>0.
结合函数f(x)的简图可得不等式的解集为 {x|0<x<3,或-3<x<0},
故选D.
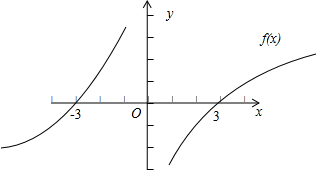 解:由条件①可得函数f(x)为(0,+∞)
解:由条件①可得函数f(x)为(0,+∞)上的增函数,
由②可得函数为奇函数,
再由③可得函数的图象过点(-3,0)、(3,0),
故由不等式x•f(x)<0可得,
当x>0时,f(x)<0;
当x<0时,f(x)>0.
结合函数f(x)的简图可得不等式的解集为 {x|0<x<3,或-3<x<0},
故选D.
点评:本题主要考查函数的奇偶性和单调性的应用,其它不等式的解法,属于中档题.

练习册系列答案
相关题目