摘要：例4.已知常数.向量.经过原点以为方向向量的直线与经过定点以为方向向量的直线相交于点.其中．试问:是否存在两个定点.使得为定值.若存在.求出的坐标,若不存在.说明理由．(本小题主要考查平面向量的概念和计算,求轨迹的方法.椭圆的方程和性质.利用方程判定曲线的性质.曲线与方程的关系等解析几何的基本思想和综合解题能力.)解:根据题设条件.首先求出点P坐标满足的方程.据此再判断是否存在两定点.使得点P到两定点距离的和为定值.∵. ∴=(λ.a).=(1.-2λa).因此.直线OP和AP的方程分别为和 .消去参数λ.得点的坐标满足方程.整理得 --① 因为所以得: (i)当时.方程①是圆方程.故不存在合乎题意的定点E和F, (ii)当时.方程①表示椭圆.焦点和为合乎题意的两个定点, (iii)当时.方程①也表示椭圆.焦点和为合乎题意的两个定点.点评:本题以平面向量为载体.考查求轨迹的方法.利用方程判定曲线的性质.曲线与方程的关系等解析几何的基本思想和综合解题能力.去掉平面向量的背景.我们不难看到.本题即为下题:在△OAP中.O为两个定点.另两边OP与AP的斜率分别是.求P的轨迹.而课本上有一道习题第96页练习题4):三角形ABC的两个顶点A.B的坐标分别是.边AC.BC所在直线的斜率之积等于.求顶点C的轨迹方程.通过本例可见高考题目与课本的密切关系.

网址：http://m.1010jiajiao.com/timu_id_78163[举报]

据权威人士分析“严格来讲，我国目前已进入负利率时代”，“钱在银行缩水”．以一年期存款利率1．98%为例，现考虑2003年物价指数上升3．2%和利息税20%两方面因素，实际利息率为-1．616%（即1．98%×(1-20%)-3．2%），这意味将100000元人民币存入银行，1年后实际价值为98384元，1616元白白“蒸发”．据初步估计2004年物价指数将上升2．2%，假设其它条件不变，请你计算一下某人2004年年初存入银行100000元，1年后的实际价值变为

A.
99464元
B.
99384元
C.
98384元
D.
100616元

查看习题详情和答案>>

21、某地区原有可退耕还林面积63.68万亩，从2000年开始执行国家退耕还林政策，当年就退耕还林8万亩，此后退耕还林的面积逐年增加，到2002年底共退耕还林29.12万亩．
（1）求2001年、2002年退耕还林面积的平均增长率．（参考数据：3.4²=11.56）
（2）该地区从2003年起加大退耕还林的力度．设2003年退耕还林的面积为y万亩，退耕还林面积的增长率为x．试写出y与x的函数关系式，并求出当y不小于14.4万亩时x的取值范围．

查看习题详情和答案>>

近年来，太阳能技术运用的步伐日益加快，已知2002年全球太阳能年生产量为670兆瓦，年增长率为34%．在此后的四年里，增长率以每年2%的速度增长（例如2003年的年生产量增长率为36%）
（1）求2006年的太阳能年生产量（精确到0.1兆瓦）
（2）已知2006年太阳能年安装量为1420兆瓦，在此后的4年里年生产量保持42%的增长率，若2010年的年安装量不少于年生产量的95%，求4年内年安装量的增长率的最小值（精确到0.1%）查看习题详情和答案>>

2003年10月15日，我国的“长征”二号F型火箭成功发射了“神州”五号载人飞船，这标志着中国人民又迈出了具有历史意义的一步．火箭的起飞重量M是箭体（包括搭载的飞行器）的重量m和燃料重量x之和．在不考虑空气阻力的条件下，假设火箭的最大速度y关于x的函数关系式为y=k[ln(m+x)-ln(

m)]+4ln2（其中k≠0，lnx是以e为底x的对数）．当燃料重量为(

-1)m吨时，该火箭的最大速度为4（km/s）．
（1）求“长征”二号系列火箭的最大速度y（km/s）与燃料重量x吨之间的函数关系式y=f（x）；
（2）已知“长征”二号F型火箭的起飞重量是479.8吨，则应装载多少吨燃料（精确到0.1吨，取e=2.718）才能使火箭的最大飞行速度达到8（km/s），顺利地把飞船发送到预定的椭圆轨道？

查看习题详情和答案>>

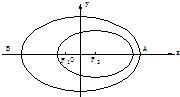2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行．该轨道是以地球的中心F₂为一个焦点的椭圆．选取坐标系如图所示，椭圆中心在原点．近地点A距地面200km，远地点B距地面350km．已知地球半径R=6371km．
（I）求飞船飞行的椭圆轨道的方程；
（II）飞船绕地球飞行了十四圈后，于16日5时59分返
回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×10⁵km，问飞船巡天飞行的平均速度是多少km/s？
（结果精确到1km/s）（注：km/s即千米/秒）查看习题详情和答案>>

试题分类