摘要:例6.数列中.且满足 ⑴求数列的通项公式,⑵设.求,⑶设=.是否存在最大的整数.使得对任意.均有成立?若存在.求出的值,若不存在.请说明理由.解:(1)由题意..为等差数列.设公差为.由题意得..(2)若.时. (3)若对任意成立.即对任意成立.的最小值是.的最大整数值是7.即存在最大整数使对任意.均有说明:本例复习数列通项.数列求和以及有关数列与不等式的综合问题..五.强化训练(一)用基本量方法解题
网址:http://m.1010jiajiao.com/timu_id_77960[举报]
已知数列![]() 的通项公式是
的通项公式是![]() ,数列
,数列![]() 是等差数列,令集合
是等差数列,令集合![]() ,
,![]() ,
,![]() .将集合
.将集合![]() 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前5项成等比数列,且
的前5项成等比数列,且![]() ,
,![]() ,求满足
,求满足![]()
的正整数![]() 的个数.
的个数.
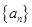 的通项公式为
的通项公式为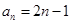 ,数列
,数列 的前
的前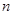 项和为
项和为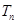 ,且满足
,且满足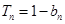 .
.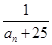 是
是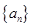 的通项公式为
的通项公式为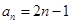 ,数列
,数列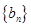 的前
的前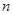 项和为
项和为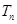 ,且满足
,且满足 .
.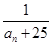 是
是