摘要：显然当.即点P位于椭圆的短轴的顶点处时.m取得最大值25. 故应填或 20 一只酒杯的轴截面是抛物线的一部分.它的函数解析式是.在杯内放一个玻璃球.要使球触及酒杯底部.则玻璃球的半径r的取值范围是 .讲解 依抛物线的对称性可知.大圆的圆心在y轴上.并且圆与抛物线切于抛物线的顶点.从而可设大圆的方程为 由 消去x.得 (*)解出 或 要使(*)式有且只有一个实数根.只要且只需要即 再结合半径.故应填
网址：http://m.1010jiajiao.com/timu_id_77732[举报]
（2012•浦东新区一模）如图所示，在平面直角坐标系xOy上放置一个边长为1的正方形PABC，此正方形PABC沿x轴滚动（向左或向右均可），滚动开始时，点P位于原点处，设顶点P（x，y）的纵坐标与横坐标的函数关系是y=f（x），x∈R，该函数相邻两个零点之间的距离为m．（1）写出m的值并求出当0≤x≤m时，点P运动路径的长度l；
（2）写出函数f（x），x∈[4k-2，4k+2]，k∈Z的表达式；研究该函数的性质并填写下面表格：
| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k，4k+2]，k∈z [4k，4k+2]，k∈z |
| 递减区间 | [4k-2，4k]，k∈z [4k-2，4k]，k∈z | |
| 零点 | x=4k，k∈z x=4k，k∈z | |
如图，已知A1，A2分别为椭圆| y2 |
| 4 |
| x2 |
| 3 |
（1）当点P位于y轴右侧，且PF∥l时，求直线A1M的方程；
（2）是否存在m值，使得以MN为直径的圆过F点？若存在加以证明，若不存在，请说明理由；
（3）由（2）问所得m值，求线段MN最小值．
已知半椭圆| x2 |
| b2 |
| y2 |
| a2 |
| x2 |
| b2 |
| y2 |
| a2 |
| ||
| 3 |
| ||
| 3 |
（1）求曲线C的方程；
（2）连PC、PD交AB分别于点E、F，求证：AE2+BF2为定值． 查看习题详情和答案>>
如图所示，在平面直角坐标系xOy上放置一个边长为1的正方形PABC，此正方形PABC沿x轴滚动（向左或向右均可），滚动开始时，点P位于原点处，设顶点P（x，y）的纵坐标与横坐标的函数关系是y=f（x），x∈R，该函数相邻两个零点之间的距离为m．
（1）写出m的值并求出当0≤x≤m时，点P运动路径的长度l；
（2）写出函数f（x），x∈[4k-2，4k+2]，k∈Z的表达式；研究该函数的性质并填写下面表格：
（3）试讨论方程f（x）=a|x|在区间[-8，8]上根的个数及相应实数a的取值范围．
查看习题详情和答案>>
（1）写出m的值并求出当0≤x≤m时，点P运动路径的长度l；
（2）写出函数f（x），x∈[4k-2，4k+2]，k∈Z的表达式；研究该函数的性质并填写下面表格：
| 函数性质 | 结 论 | |
| 奇偶性 | ______ | |
| 单调性 | 递增区间 | ______ |
| 递减区间 | ______ | |
| 零点 | ______ | |
查看习题详情和答案>>
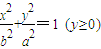和半圆x2+y2=b2（y≤0）组成曲线C，其中a＞b＞0；如图，半椭圆
内切于矩形ABCD，且CD交y轴于点G，点P是半圆x2+y2=b2（y≤0）上异于A，B的任意一点，当点P位于点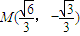
时，△AGP的面积最大．