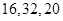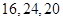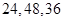摘要:(Ⅱ)为线段上一点.直线垂直直线.且交圆于点.过点的切线交直线于.证明:.解:(Ⅰ)证明:因为是圆的切线.所以.又因为.在中.由射影定理知..(Ⅱ)证明:因为是圆的切线..同(Ⅰ).有.又.所以.即.又.所以.故.
网址:http://m.1010jiajiao.com/timu_id_77461[举报]
“点动成线,线动成面,面动成体”。如图,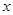 轴上有一条单位长度的线段
轴上有一条单位长度的线段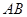 ,沿着与其垂直的
,沿着与其垂直的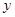 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形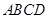 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的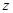 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体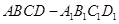 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有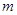 个顶点,
个顶点,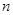 条棱,
条棱,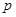 个面,则
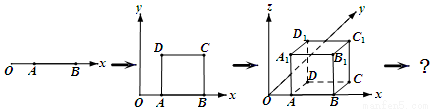
个面,则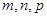 的值分别为
( )
的值分别为
( )
A.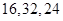 B.
B.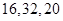 C.
C.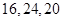 D.
D.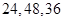
查看习题详情和答案>>
已知点 ,
, 、
、 、
、 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且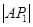 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,
, .
.
(1)若 坐标为
坐标为 ,
, ,点
,点 在直线
在直线 上时,求点
上时,求点 的坐标;
的坐标;
(2)已知圆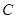 的方程是
的方程是
 ,过点
,过点 的直线交圆于
的直线交圆于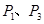 两点,
两点,
 是圆
是圆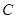 上另外一点,求实数
上另外一点,求实数 的取值范围;
的取值范围;
(3)若 、
、 、
、 都在抛物线
都在抛物线 上,点
上,点 的横坐标为
的横坐标为 ,求证:线段
,求证:线段 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标.
查看习题详情和答案>>
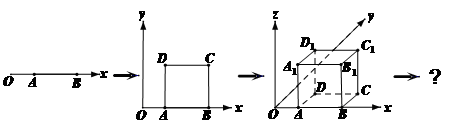
“点动成线,线动成面,面动成体”。如图,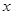 轴上有一条单位长度的线段
轴上有一条单位长度的线段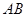 ,沿着与其垂直的
,沿着与其垂直的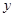 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形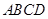 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的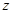 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体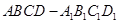 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有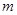 个顶点,
个顶点,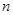 条棱,
条棱,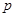 个面,则
个面,则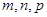 的值分别为
▲ .
的值分别为
▲ .
查看习题详情和答案>>
 ,
, 、
、 、
、 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,
, .
. ,
,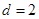 ,点
,点 上时,求点
上时,求点 的方程是
的方程是
 ,过点
,过点 的直线交圆于
的直线交圆于 两点,
两点, 是圆
是圆 上,点
上,点 ,求证:线段
,求证:线段 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标. 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的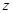 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体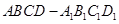 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有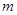 个顶点,
个顶点,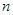 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )