摘要:在直角坐标系xOy中.椭圆C1:的左.右焦点分别为F1.F2.F2也是抛物线C2:的焦点.点M为C1与C2在第一象限的交点.且.(1)求C1的方程,(2)平面上的点N满足.直线l∥MN.且与C1交于A.B两点.若?=0.求直线l的方程.
网址:http://m.1010jiajiao.com/timu_id_77426[举报]
(本小题满分12分)
在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|![]() |>|
|>|![]() |.
|.
(本小题满分12分)
在直角坐标 系
系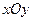 中,以
中,以 为极点,
为极点,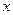 正半轴为极轴建立极坐标系,曲线
正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,
,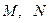 分别为
分别为 与
与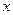 轴,
轴, 轴的交点。曲线
轴的交点。曲线 的参数方程为
的参数方程为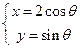 (
(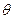 为参数)。
为参数)。
(1)求 的极坐标,并写出
的极坐标,并写出 的直角坐标
的直角坐标 方程;
方程;
(2)求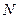 点与曲线
点与曲线 上的动点距离的最大值。
上的动点距离的最大值。
 ,
,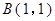 ,
, 为坐标原点,
为坐标原点,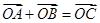 ,
,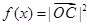 .
.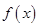 的对称中心的坐标及其在区间
的对称中心的坐标及其在区间 上的单调递减区间;
上的单调递减区间;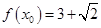 ,
,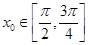 ,求
,求 的值。
的值。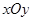 中,以
中,以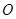 为圆心的圆与直线
为圆心的圆与直线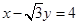 相切.
相切.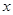 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点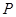 使
使 成等比数列,求
成等比数列,求 的取值范围.
的取值范围.