摘要：A．AB=DE B．∠ACE=∠DFBC．BF=EC D．∠ABC=∠DEF
网址：http://m.1010jiajiao.com/timu_id_771271[举报]
5、如图，玲玲在美术课上用丝线绣成了一个“2”，AB∥DE，∠A=30°，∠ACE=110°，则∠E的度数为（ ）
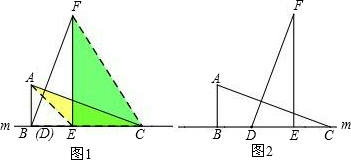
阅读：如图1，在△ABC和△DEF中，∠ABC=∠DEF=90°，AB=DE=a，BC=EF=b（a＜b），B、C、D、E四点都在直线m上，点B与点D重合．
连接AE、FC，我们可以借助于S△ACE和S△FCE的大小关系证明不等式：a2+b2＞2ab（b＞a＞0）．
证明过程如下：
∵BC=b，BE=a，EC=b-a．
∴S△ACE=
EC•AB=
(b-a)a，S△FCE=
EC•FE=
(b-a)b．
∵b＞a＞0
∴S△FCE＞S△ACE
即
(b-a)b＞
(b-a)a
∴b2-ab＞ab-a2
∴a2+b2＞2ab
解决下列问题：
（1）现将△DEF沿直线m向右平移，设BD=k（b-a），且0≤k≤1．如图2，当BD=EC时，k= ．利用此图，仿照上述方法，证明不等式：a2+b2＞2ab（b＞a＞0）．
（2）用四个与△ABC全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式．请你画出一个示意图，并简要说明理由．
查看习题详情和答案>>
连接AE、FC，我们可以借助于S△ACE和S△FCE的大小关系证明不等式：a2+b2＞2ab（b＞a＞0）．
证明过程如下：
∵BC=b，BE=a，EC=b-a．
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵b＞a＞0
∴S△FCE＞S△ACE
即
| 1 |
| 2 |
| 1 |
| 2 |
∴b2-ab＞ab-a2
∴a2+b2＞2ab
解决下列问题：
（1）现将△DEF沿直线m向右平移，设BD=k（b-a），且0≤k≤1．如图2，当BD=EC时，k=
（2）用四个与△ABC全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式．请你画出一个示意图，并简要说明理由．
查看习题详情和答案>>
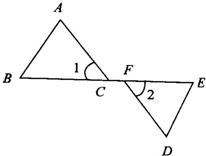5、如图所示，∠1=∠2，BC=EF，欲证△ABC≌△DEF，则还须补充的一个条件是（ ）
如图，点B、E、C、F在同一直线上，且AB=DE，AC=DF，BE=CF，请将下面说明∠A=∠D的过程和理由补充完整．
49、如图，已知AB⊥BD，垂足为B，ED⊥BD，垂足为D，AB=CD，BC=DE，则∠ACE=