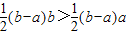题目内容
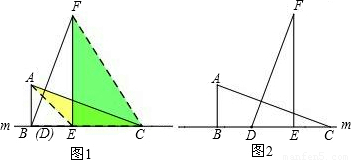
阅读:如图1,在△ABC和△DEF中,∠ABC=∠DEF=90°,AB=DE=a,BC=EF=b(a<b),B、C、D、E四点都在直线m上,点B与点D重合.连接AE、FC,我们可以借助于S△ACE和S△FCE的大小关系证明不等式:a2+b2>2ab(b>a>0).
证明过程如下:
∵BC=b,BE=a,EC=b-a.
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵b>a>0
∴S△FCE>S△ACE
即
| 1 |
| 2 |
| 1 |
| 2 |
∴b2-ab>ab-a2
∴a2+b2>2ab
解决下列问题:
(1)现将△DEF沿直线m向右平移,设BD=k(b-a),且0≤k≤1.如图2,当BD=EC时,k=
(2)用四个与△ABC全等的直角三角形纸板进行拼接,也能够借助图形证明上述不等式.请你画出一个示意图,并简要说明理由.
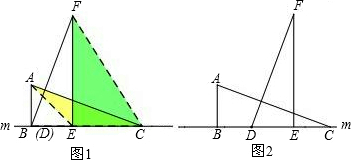
分析:(1)连接AD、BF,构成同底的两个三角形,再利用两个三角形的边之间的关系,代入三角形的面积公式求解即可;
(2)答案不唯一,举例说明:根据直角三角形及矩形的面积公式求得面积后,再根据它们之间的数量关系来比较.
(2)答案不唯一,举例说明:根据直角三角形及矩形的面积公式求得面积后,再根据它们之间的数量关系来比较.
解答:解:(1)k=
;
证明:连接AD、BF.
可得BD=
(b-a),
∴S△ABD=
BD•AB
=
×
×(b-a)•a
=
a(b-a)S△FBD
=
BD•FE
=
×
×(b-a)•b
=
b(b-a).
∵b>a>0,∴S△ABD<S△FBD,即
a(b-a)<
b(b-a),
∴ab-a2<b2-ab.∴a2+b2>2ab;
(2)答案不唯一,图(1分),理由:
举例:如图,理由:
延长BA、FE交于点I.
∵b>a>0,∴S矩形IBCE>S矩形ABCD,
即b(b-a)>a(b-a).
∴b2-ab>ab-a2.
∴a2+b2>2ab.
举例:如图,理由:
四个直角三角形的面积和S1=4×
a•b=2ab,
大正方形的面积S2=a2+b2.∵b>a>0,∴S2>S1.∴a2+b2>2ab.
| 1 |
| 2 |
证明:连接AD、BF.
可得BD=
| 1 |
| 2 |
∴S△ABD=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
∵b>a>0,∴S△ABD<S△FBD,即
| 1 |
| 4 |
| 1 |
| 4 |
∴ab-a2<b2-ab.∴a2+b2>2ab;
(2)答案不唯一,图(1分),理由:
举例:如图,理由:
延长BA、FE交于点I.
∵b>a>0,∴S矩形IBCE>S矩形ABCD,
即b(b-a)>a(b-a).
∴b2-ab>ab-a2.
∴a2+b2>2ab.
举例:如图,理由:
四个直角三角形的面积和S1=4×
| 1 |
| 2 |
大正方形的面积S2=a2+b2.∵b>a>0,∴S2>S1.∴a2+b2>2ab.

点评:做这类题目时,结合图形来解答会降低题的难度.

练习册系列答案
相关题目

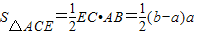 ,
, .
.