网址:http://m.1010jiajiao.com/timu_id_77105[举报]
一、选择题:C D C C A D B B
1.C【解析】含详解.files/image298.gif) ,而
,而含详解.files/image300.gif) ,即
,即含详解.files/image302.gif) ,
,含详解.files/image304.gif)
2.D【解析】含详解.files/image306.gif) ,
,含详解.files/image308.gif) ,故
,故含详解.files/image310.gif)
3.C【解析】依题意我们知道二年级的女生有380人,那么三年级的学生的人数应该是含详解.files/image312.gif) ,即总体中各个年级的人数比例为
,即总体中各个年级的人数比例为含详解.files/image314.gif) ,故在分层抽样中应在三年级抽取的学生人数为
,故在分层抽样中应在三年级抽取的学生人数为含详解.files/image316.gif)
4.C 5.A
6.D【解析】不难判断命题含详解.files/image318.gif) 为真命题,命题
为真命题,命题含详解.files/image320.gif) 为假命题,从而上述叙述中只有
为假命题,从而上述叙述中只有含详解.files/image322.gif) 为真命题
为真命题
7.B【解析】含详解.files/image324.gif) ,若函数在
,若函数在含详解.files/image326.gif) 上有大于零的极值点,即
上有大于零的极值点,即含详解.files/image328.gif) 有正根。当有
有正根。当有含详解.files/image328.gif) 成立时,显然有
成立时,显然有含详解.files/image330.gif) ,此时
,此时含详解.files/image332.gif) ,由
,由含详解.files/image334.gif) 我们马上就能得到参数
我们马上就能得到参数含详解.files/image015.gif) 的范围为
的范围为含详解.files/image337.gif) 。
。
8.B
二、填空题:
9.【解析】要结束程序的运算,就必须通过含详解.files/image007.gif) 整除
整除含详解.files/image015.gif) 的条件运算,而同时
的条件运算,而同时含详解.files/image341.gif) 也整除
也整除含详解.files/image015.gif) ,那么
,那么含详解.files/image015.gif) 的最小值应为
的最小值应为含详解.files/image341.gif) 和
和含详解.files/image007.gif) 的最小公倍数12,即此时有
的最小公倍数12,即此时有含详解.files/image344.gif) 。
。
10.【解析】含详解.files/image130.gif) 按二项式定理展开的通项为
按二项式定理展开的通项为含详解.files/image347.gif) ,我们知道
,我们知道含详解.files/image134.gif) 的系数为
的系数为含详解.files/image350.gif) ,即
,即含详解.files/image352.gif) ,也即
,也即含详解.files/image354.gif) ,而
,而含详解.files/image132.gif) 是正整数,故
是正整数,故含详解.files/image132.gif) 只能取1。
只能取1。
11.【解析】易知点C为含详解.files/image357.gif) ,而直线与
,而直线与含详解.files/image359.gif) 垂直,我们设待求的直线的方程为
垂直,我们设待求的直线的方程为含详解.files/image361.gif) ,将点C的坐标代入马上就能求出参数
,将点C的坐标代入马上就能求出参数含详解.files/image363.gif) 的值为
的值为含详解.files/image365.gif) ,故待求的直线的方程为
,故待求的直线的方程为含详解.files/image367.gif) 。
。
12.【解析】含详解.files/image369.gif) ,故函数的最小正周期
,故函数的最小正周期含详解.files/image371.gif) 。
。
二、选做题(13―15题,考生只能从中选做两题)
13.【解析】由含详解.files/image373.gif) 解得
解得含详解.files/image375.gif) ,即两曲线的交点为
,即两曲线的交点为含详解.files/image377.gif) 。
。
14.含详解.files/image379.gif)
15.【解析】依题意,我们知道含详解.files/image381.gif) ,由相似三角形的性质我们有
,由相似三角形的性质我们有含详解.files/image383.gif) ,即
,即含详解.files/image385.gif) 。
。
三、解答题:本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤.
16.解:(1)依题意有含详解.files/image387.gif) ,则
,则含详解.files/image389.gif) ,将点
,将点含详解.files/image391.gif) 代入得
代入得含详解.files/image393.gif) ,而
,而含详解.files/image395.gif) ,
,含详解.files/image397.gif) ,
,含详解.files/image399.gif) ,故
,故含详解.files/image401.gif) ;
;
(2)依题意有含详解.files/image403.gif) ,而
,而含详解.files/image405.gif) ,
,
含详解.files/image407.gif) ,
,
含详解.files/image409.gif) 。
。
17.解:(1)含详解.files/image198.gif) 的所有可能取值有6,2,1,-2;
的所有可能取值有6,2,1,-2;含详解.files/image412.gif) ,
,含详解.files/image414.gif)
含详解.files/image416.gif) ,
,含详解.files/image418.gif)
故含详解.files/image198.gif) 的分布列为:
的分布列为:
含详解.files/image198.gif)
6
2
1
-2
含详解.files/image220.gif)
0.63
0.25
0.1
0.02
(2)含详解.files/image422.gif)
(3)设技术革新后的三等品率为含详解.files/image038.gif) ,则此时1件产品的平均利润为
,则此时1件产品的平均利润为
含详解.files/image425.gif)
依题意,含详解.files/image427.gif) ,即
,即含详解.files/image429.gif) ,解得
,解得含详解.files/image431.gif)
含详解.files/image432.gif) 所以三等品率最多为
所以三等品率最多为含详解.files/image434.gif)
18.解:(1)由含详解.files/image209.gif) 得
得含详解.files/image437.gif) ,
,
当含详解.files/image439.gif) 得
得含详解.files/image441.gif) ,
,含详解.files/image443.gif) G点的坐标为
G点的坐标为含详解.files/image445.gif) ,
,
含详解.files/image447.gif) ,
, 含详解.files/image449.gif) ,
,
过点G的切线方程为含详解.files/image451.gif) 即
即含详解.files/image453.gif) ,
,
令含详解.files/image455.gif) 得
得含详解.files/image457.gif) ,
,含详解.files/image459.gif) 点的坐标为
点的坐标为含详解.files/image461.gif) ,
,
由椭圆方程得含详解.files/image217.gif) 点的坐标为
点的坐标为含详解.files/image464.gif) ,
,含详解.files/image466.gif) 即
即含详解.files/image365.gif) ,
,
即椭圆和抛物线的方程分别为含详解.files/image469.gif) 和
和含详解.files/image471.gif) ;
;
(2)含详解.files/image473.gif) 过
过含详解.files/image168.gif) 作
作含详解.files/image038.gif) 轴的垂线与抛物线只有一个交点
轴的垂线与抛物线只有一个交点含详解.files/image220.gif) ,
,
含详解.files/image443.gif) 以
以含详解.files/image479.gif) 为直角的
为直角的含详解.files/image481.gif) 只有一个,同理
只有一个,同理含详解.files/image443.gif) 以
以含详解.files/image483.gif) 为直角的
为直角的含详解.files/image481.gif) 只有一个。
只有一个。
若以含详解.files/image485.gif) 为直角,设
为直角,设含详解.files/image220.gif) 点坐标为
点坐标为含详解.files/image488.gif) ,
,含详解.files/image168.gif) 、
、含详解.files/image177.gif) 两点的坐标分别为
两点的坐标分别为含详解.files/image492.gif) 和
和含详解.files/image494.gif) ,
,
含详解.files/image496.gif) 。
。
关于含详解.files/image498.gif) 的二次方程有一大于零的解,
的二次方程有一大于零的解,含详解.files/image500.gif) 有两解,即以
有两解,即以含详解.files/image485.gif) 为直角的
为直角的含详解.files/image481.gif) 有两个,
有两个,
因此抛物线上存在四个点使得含详解.files/image502.gif) 为直角三角形。
为直角三角形。
19.解: 含详解.files/image504.gif) ,
,含详解.files/image506.gif)
对于含详解.files/image508.gif) ,
,
当含详解.files/image510.gif) 时,函数
时,函数含详解.files/image231.gif) 在
在含详解.files/image513.gif) 上是增函数;
上是增函数;
当含详解.files/image515.gif) 时,函数
时,函数含详解.files/image231.gif) 在
在含详解.files/image517.gif) 上是减函数,在
上是减函数,在含详解.files/image519.gif) 上是增函数;
上是增函数;
对于含详解.files/image521.gif) ,
,
当含详解.files/image523.gif) 时,函数
时,函数含详解.files/image231.gif) 在
在含详解.files/image525.gif) 上是减函数;
上是减函数;
当含详解.files/image527.gif) 时,函数
时,函数含详解.files/image231.gif) 在
在含详解.files/image529.gif) 上是减函数,在
上是减函数,在含详解.files/image531.gif) 上是增函数。
上是增函数。
含详解.files/image532.gif) 20.解:(1)在
20.解:(1)在含详解.files/image534.gif) 中,
中,
含详解.files/image536.gif) ,
,含详解.files/image538.gif)
而PD垂直底面ABCD,含详解.files/image540.gif)
含详解.files/image542.gif) ,
,
在含详解.files/image544.gif) 中,
中,含详解.files/image546.gif) ,即
,即含详解.files/image544.gif) 为以
为以含详解.files/image479.gif) 为直角的直角三角形。
为直角的直角三角形。
设点含详解.files/image549.gif) 到面
到面含详解.files/image551.gif) 的距离为
的距离为含详解.files/image553.gif) ,
,
由含详解.files/image555.gif) 有
有含详解.files/image557.gif) ,
,
即 含详解.files/image559.gif) ,
,
含详解.files/image561.gif) ;
;
(2)含详解.files/image563.gif) ,而
,而含详解.files/image565.gif) ,
,
即含详解.files/image567.gif) ,
,含详解.files/image569.gif) ,
,含详解.files/image571.gif) ,
,含详解.files/image573.gif) 是直角三角形;
是直角三角形;
(3)含详解.files/image575.gif) 时
时含详解.files/image577.gif) ,
,含详解.files/image579.gif) ,
,
即含详解.files/image581.gif) ,
,
含详解.files/image573.gif) 的面积
的面积含详解.files/image584.gif)
21.解:(1)由求根公式,不妨设含详解.files/image586.gif) ,得
,得含详解.files/image588.gif)
含详解.files/image590.gif) ,
,含详解.files/image592.gif)
(2)设含详解.files/image594.gif) ,则
,则含详解.files/image596.gif) ,由
,由含详解.files/image282.gif)
得,含详解.files/image598.gif) ,消去
,消去含详解.files/image600.gif) ,得
,得含详解.files/image602.gif) ,
,含详解.files/image604.gif) 是方程
是方程含详解.files/image274.gif) 的根,
的根,
由题意可知,含详解.files/image606.gif)
①当含详解.files/image608.gif) 时,此时方程组
时,此时方程组含详解.files/image609.gif) 的解记为
的解记为含详解.files/image611.gif)
含详解.files/image613.gif)
含详解.files/image615.gif)
即含详解.files/image617.gif) 、
、含详解.files/image619.gif) 分别是公比为
分别是公比为含详解.files/image621.gif) 、
、含详解.files/image623.gif) 的等比数列,
的等比数列,
由等比数列性质可得含详解.files/image625.gif) ,
,含详解.files/image627.gif) ,
,
两式相减,得含详解.files/image629.gif)
含详解.files/image631.gif) ,
,含详解.files/image633.gif) ,
,含详解.files/image635.gif)
含详解.files/image637.gif) ,
,含详解.files/image639.gif)
含详解.files/image641.gif) ,即
,即含详解.files/image643.gif) ,
,含详解.files/image645.gif)
②当含详解.files/image647.gif) 时,即方程
时,即方程含详解.files/image274.gif) 有重根,
有重根,含详解.files/image649.gif) ,
,
即含详解.files/image651.gif) ,得
,得含详解.files/image653.gif) ,不妨设
,不妨设含详解.files/image655.gif) ,由①可知
,由①可知
含详解.files/image625.gif) ,
,含详解.files/image657.gif) ,
,含详解.files/image659.gif)
即含详解.files/image661.gif) ,等式两边同时除以
,等式两边同时除以含详解.files/image663.gif) ,得
,得含详解.files/image665.gif) ,即
,即含详解.files/image667.gif)
含详解.files/image443.gif) 数列
数列含详解.files/image670.gif) 是以1为公差的等差数列,
是以1为公差的等差数列,含详解.files/image672.gif)
含详解.files/image674.gif)
综上所述,含详解.files/image676.gif)
(3)把含详解.files/image291.gif) ,
,含详解.files/image293.gif) 代入
代入含详解.files/image274.gif) ,得
,得含详解.files/image678.gif) ,解得
,解得含详解.files/image680.gif)
含详解.files/image682.gif)
含详解.files/image684.gif)
含详解.files/image686.gif)
含详解.files/image688.gif)
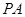 是圆
是圆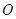 的切线,切点为
的切线,切点为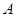 ,直线
,直线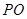 交圆
交圆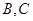 两点,
两点, ,
,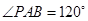 ,则圆
,则圆
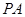 是圆
是圆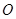 的切线,切点为
的切线,切点为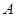 ,直线
,直线 交圆
交圆 两点,
两点, ,
, ,则圆
,则圆
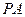 是圆
是圆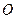 的切线,切点为
的切线,切点为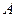 ,
,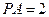 .
.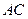 是圆
是圆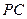 与圆
与圆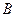 点,
点,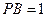 ,则圆
,则圆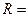 .
.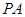 是圆
是圆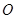 的切线,切点为
的切线,切点为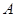 ,直线
,直线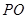 交圆
交圆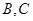 两点,
两点,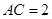 ,
,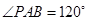 ,则圆
,则圆