摘要:14.由两条对角线分成的四个三角形一定都相互全等的四边形是 .
网址:http://m.1010jiajiao.com/timu_id_769889[举报]
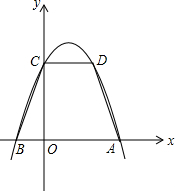 如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=
如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=| 10 |
(1)求抛物线的函数表达式;
(2)点E是x轴上一点,且以E、A、D、C为顶点的四边形是平行四边形.若过B点的直线把这个四边形的面积分成相等的两部分,求该直线的函数表达式;
(3)P是抛物线对称轴上一点,连接PC、PA,是否存在△PAC是直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
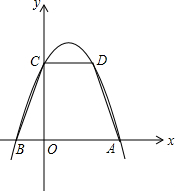 如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=
如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC= ,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.
,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.