题目内容
14、由两条对角线分成的四个三角形一定都相互全等的四边形是
菱形
.分析:由题意,要是4个三角形都全等,在一条对角线一边的的两个三角形必须相等,要求两条对角线垂直,而对定的两个三角形全等则要求对角线互相平分,即综合考虑可知是菱形.
解答: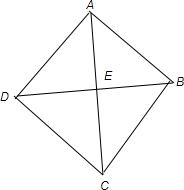 解:如图所示,△ABE≌△CBE
解:如图所示,△ABE≌△CBE
则AB=BC AE=CE
∵△ABE≌△CDE
∴AB=CD BE=DE
同理可以证得BC=AD AE=CE
∴AB=BC=CD=DA
∵AE=CE BE=DE
∴ABCD为菱形.
故答案为菱形.
 解:如图所示,△ABE≌△CBE
解:如图所示,△ABE≌△CBE则AB=BC AE=CE
∵△ABE≌△CDE
∴AB=CD BE=DE
同理可以证得BC=AD AE=CE
∴AB=BC=CD=DA
∵AE=CE BE=DE
∴ABCD为菱形.
故答案为菱形.
点评:做此类题要先画出草图,由图形辅助分析清晰明了,还要敢于猜测可能的答案,然后证明.

练习册系列答案
相关题目
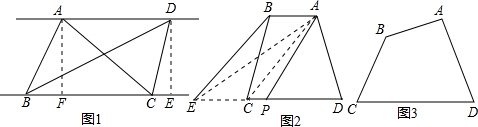
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=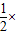 BC×DE
BC×DE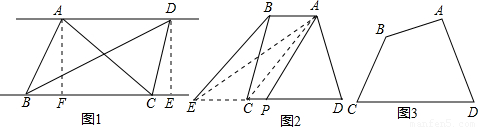
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=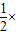 BC×DE
BC×DE