摘要：八. 若a.b互为相反数.c.d互为倒数.x的绝对值等于它相反数的2倍．求x3+abcdx+a+bcd的值.
网址：http://m.1010jiajiao.com/timu_id_768624[举报]
（本大题有两题，请同学们选择你喜欢且拿手一题解答）
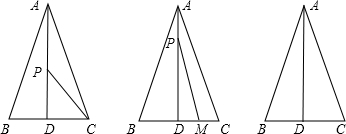
【Ⅰ】如图，在△ABC中，AB=AC=13厘米，BC=10厘米，AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动．设动点运动时间为t秒．
（1）求AD的长；
（2）当△PDC的面积为15平方厘米时，求t的值；
（3）动点M从点C出发以每秒2厘米的速度在射线CB上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得S△PMD=
S△ABC？若存在，请求出t的值；若不存在，请说明理由．
【Ⅱ】我校工会于“三•八”妇女节期间组织女职工到国家级风景区“文成铜铃山”观光旅游．下面是领队与旅行社导游收费标准的一段对话：
【领队】组团去“文成铜铃山”旅游每人收费是多少？
【导游】如果人数不超过30人，人均旅游费用为360元．
【领队】超过30人怎样优惠呢？
【导游】如果超过30人，每增加1人，人均旅游费用降低5元，但人均旅游费用不得低于300元．
我校按旅行社的收费标准组团浏览“文成铜铃山”结束后，共支付给旅行社12400元．设我校这次参加旅游的共有x人．
请你根据上述信息，回答下列问题：
（1）我校参加旅游的人数x的取值范围是 ；
（2）我校参加旅游的人每人实际应收费 元（用含x的代数式表示）；
（3）求我校这次到“文成铜铃山”观光旅游的女职工共有多少人？ 查看习题详情和答案>>
【Ⅰ】如图，在△ABC中，AB=AC=13厘米，BC=10厘米，AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动．设动点运动时间为t秒．
（1）求AD的长；
（2）当△PDC的面积为15平方厘米时，求t的值；
（3）动点M从点C出发以每秒2厘米的速度在射线CB上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得S△PMD=
| 1 | 12 |
【Ⅱ】我校工会于“三•八”妇女节期间组织女职工到国家级风景区“文成铜铃山”观光旅游．下面是领队与旅行社导游收费标准的一段对话：
【领队】组团去“文成铜铃山”旅游每人收费是多少？
【导游】如果人数不超过30人，人均旅游费用为360元．
【领队】超过30人怎样优惠呢？
【导游】如果超过30人，每增加1人，人均旅游费用降低5元，但人均旅游费用不得低于300元．
我校按旅行社的收费标准组团浏览“文成铜铃山”结束后，共支付给旅行社12400元．设我校这次参加旅游的共有x人．
请你根据上述信息，回答下列问题：
（1）我校参加旅游的人数x的取值范围是
（2）我校参加旅游的人每人实际应收费
（3）求我校这次到“文成铜铃山”观光旅游的女职工共有多少人？ 查看习题详情和答案>>
附加题：
友情提示：你已完成上面全部试题，请再认真检查一遍，并自我评价得分情况．如果你估计全卷得分低于 90 分，请再完成本大题，将补加 0～10 分，并计入总分，但计入后全卷总分最多不超过 90 分；如果你全卷得分已经达到或超过 90 分，本大题将不再进行批阅．
（1）计算：
+
-
（2）解方程：x2-20=0．
查看习题详情和答案>>
友情提示：你已完成上面全部试题，请再认真检查一遍，并自我评价得分情况．如果你估计全卷得分低于 90 分，请再完成本大题，将补加 0～10 分，并计入总分，但计入后全卷总分最多不超过 90 分；如果你全卷得分已经达到或超过 90 分，本大题将不再进行批阅．
（1）计算：
| 45 |
| 20 |
| 5 |
（2）解方程：x2-20=0．
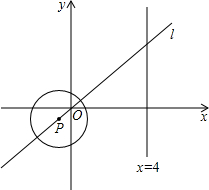如图，P为正比例函数y=| 3 | 4 |
（1）求⊙P与直线x=4相切时m、n的值；
（2）写出⊙P与直线x=4相交、相离时m的取值范围；
（3）若⊙P从原点出发，以每秒1个单位的速度沿直线l：向右上方向运动，同时圆的半径逐渐增大，半径r与运动时间t（秒）的关系为r=t+2．则当t取何值时，⊙P与直线l相切？（本大题不必写过程，直接写出结论）
设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：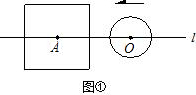
所以，当r＜a时，⊙O与正方形的公共点的个数可能有 个；
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：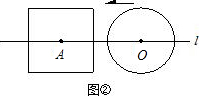
所以，当r=a时，⊙O与正方形的公共点个数可能有 个；
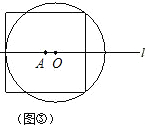
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
a；
（4）就r＞a的情形，请你仿照“当…时，⊙O与正方形的公共点个数可能有 个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）．
查看习题详情和答案>>
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a+r | |
d=a+r |
|
| a≤d＜a+r | |
| d=a-r | |
| d＜a-r |
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a+r | |
| d=a+r | |
| a≤d＜a+r | |
| d＜a |
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
| 5 |
| 4 |
（4）就r＞a的情形，请你仿照“当…时，⊙O与正方形的公共点个数可能有
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）．
查看习题详情和答案>>