摘要：结论:在≥(a.b均为正实数)中.若ab为定值p.则a+b≥.只有当a＝b时.a+b有最小值．(1)根据上述内容.回答下列问题:
网址：http://m.1010jiajiao.com/timu_id_764653[举报]
阅读理对于任意正实数a、b，∵(
-
)2≥0，∴a-2
+b≥0，∴a+b≥2
，只有当a=b时，等号成立．
结论：在a+b≥2
（a、b均为正实数）中，若ab为定值p，则a+b≥2
，只有当a=b时，a+b有最小值2
．
根据上述内容，回答：若m＞0，只有当m=______时，m+
有最小值______．
查看习题详情和答案>>
| a |
| b |
| ab |
| ab |
结论：在a+b≥2
| ab |
| p |
| p |
根据上述内容，回答：若m＞0，只有当m=______时，m+
| 1 |
| m |
阅读理解
对于任意正实数a，b，∵(
-
)2≥0，∴a+b-2
≥0，∴a+b≥2
，只有当a=b时，等号成立．
结论：在a+b≥2
（a，b均为正实数）中，若ab为定值p，则a+b≥2
只有当a=b时，a+b有最小值2
．
根据上述内容，回答下列问题：
（1）若m＞0，只有当m= 时，m+
有最小值 ．
（2）探索应用
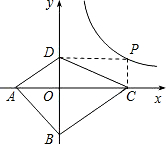
如图，已知A（-2，0），B（0，-3），P为双曲线y=
（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．
（3）实践应用
建筑一个容积为800m3，深为8m的长方体蓄水池，池壁每平方米造价为80元，池底每平方米造价为120元，如何设计池底的长、宽，使总造价最低？ 查看习题详情和答案>>
对于任意正实数a，b，∵(
| a |
| b |
| ab |
| ab |
结论：在a+b≥2
| ab |
| p |
| p |
根据上述内容，回答下列问题：
（1）若m＞0，只有当m=
| 1 |
| m |
（2）探索应用
如图，已知A（-2，0），B（0，-3），P为双曲线y=
| 6 |
| x |
（3）实践应用
建筑一个容积为800m3，深为8m的长方体蓄水池，池壁每平方米造价为80元，池底每平方米造价为120元，如何设计池底的长、宽，使总造价最低？ 查看习题详情和答案>>
阅读理解：对于任意正实数a、b，∵(
-
)2≥0，∴a-2
+b≥0，∴a+b≥2
，只有当a=b时，等号成立．
结论：在a+b≥2
（a、b均为正实数）中，若ab为定值p，则a+b≥2
，只有当a=b时，a+b有最小值2
．
根据上述内容，回答：若m＞0，只有当m= 时，m+
有最小值 ．
查看习题详情和答案>>
| a |
| b |
| ab |
| ab |
结论：在a+b≥2
| ab |
| p |
| p |
根据上述内容，回答：若m＞0，只有当m=
| 1 |
| m |
阅读理解：对于任意正实数a、b，∵(
-
)2≥0，∴a-2
+b≥0，∴a+b≥2
，只有当a=b时，等号成立．
结论：在a+b≥2
（a、b均为正实数）中，若ab为定值p，则a+b≥2
，只有当a=b时，a+b有最小值2
．
根据上述内容，回答下列问题：
（1）若m＞0，只有当m= 时，m+
有最小值
．
（2）若m＞0，只有当m= 时，2m+
有最小值
．
查看习题详情和答案>>
| a |
| b |
| ab |
| ab |
结论：在a+b≥2
| ab |
| p |
| p |
根据上述内容，回答下列问题：
（1）若m＞0，只有当m=
| 1 |
| m |
（2）若m＞0，只有当m=
| 8 |
| m |
阅读理解：对于任意正实数a、b，∵(
-
)2≥0，∴a-2
+b≥0，∴a+b≥2
，只有当a=b时，等号成立．
结论：在a+b≥2
（a、b均为正实数）中，若ab为定值p，则a+b≥2
，只有当a=b时，a+b有最小值2
．
根据上述内容，回答下列问题：
（1）若m＞0，只有当m= 时，m+
有最小值 ；
若m＞0，只有当m= 时，2m+
有最小值 ．
（2）如图，已知直线L1：y=
x+1与x轴交于点A，过点A的另一直线L2与双曲线y=
(x＞0)相交于点B（2，m），求直线L2的解析式．
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试求当线段CD最短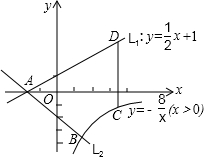
时，点A、B、C、D围成的四边形面积．
查看习题详情和答案>>
| a |
| b |
| ab |
| ab |
结论：在a+b≥2
| ab |
| p |
| p |
根据上述内容，回答下列问题：
（1）若m＞0，只有当m=
| 1 |
| m |
若m＞0，只有当m=
| 8 |
| m |
（2）如图，已知直线L1：y=
| 1 |
| 2 |
| -8 |
| x |
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试求当线段CD最短
时，点A、B、C、D围成的四边形面积．
查看习题详情和答案>>