题目内容
阅读理解:对于任意正实数a、b,∵(| a |
| b |
| ab |
| ab |
结论:在a+b≥2
| ab |
| p |
| p |
根据上述内容,回答下列问题:
(1)若m>0,只有当m=
| 1 |
| m |
若m>0,只有当m=
| 8 |
| m |
(2)如图,已知直线L1:y=
| 1 |
| 2 |
| -8 |
| x |
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1于点D,试求当线段CD最短
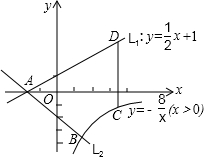 时,点A、B、C、D围成的四边形面积.
时,点A、B、C、D围成的四边形面积.
分析:(1)根据式子特殊性可以分别求出m的值以及分式的最值;
(2)首先求出直线L1与x轴的交点坐标,再利用点B(2,m)在y=
(x>0)上,求出m的值,从而求出直线L2的解析式;
(3)将四边形分割为S四ABCD=S△ABE+S四BEDC,分别求出即可.
(2)首先求出直线L1与x轴的交点坐标,再利用点B(2,m)在y=
| -8 |
| x |
(3)将四边形分割为S四ABCD=S△ABE+S四BEDC,分别求出即可.
解答: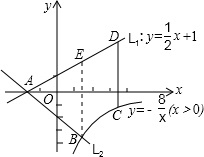 解:(1)∵m>0,只有当m=1时,m+
解:(1)∵m>0,只有当m=1时,m+
有最小值是2;
若m>0,只有当m=2时,2m+
有最小值 8.
故答案为:1,2;2,8;
(2)对于y=
x+1,令y=0,
得:x=-2,
∴A(-2,0)
又点B(2,m)在y=
(x>0)上,
∴m=-4,B(2,-4)
设直线L2的解析式为:y=kx+b,
则有
,
解得:
∴直线L2的解析式为:y=-x-2;
(3)设C(n,
),则:D(n,
n+1),
∴CD=(
n+1)-
=
n+
+1≥2
+1=5,
∴CD最短为5,
此时
n=
,n=4,C(4,-2),D(4,3)
过点B作BE∥y轴交AD于点E,则B(2,-4),E(2,2),BE=6,
∴S四边形ABCD=S△ABE+S四边形BEDC=
×6×4+
(5+6)×2=12+11=23.
 解:(1)∵m>0,只有当m=1时,m+
解:(1)∵m>0,只有当m=1时,m+| 1 |
| m |
若m>0,只有当m=2时,2m+
| 8 |
| m |
故答案为:1,2;2,8;
(2)对于y=
| 1 |
| 2 |
得:x=-2,
∴A(-2,0)
又点B(2,m)在y=
| -8 |
| x |
∴m=-4,B(2,-4)
设直线L2的解析式为:y=kx+b,
则有
|
解得:
|
∴直线L2的解析式为:y=-x-2;
(3)设C(n,
| -8 |
| n |
| 1 |
| 2 |
∴CD=(
| 1 |
| 2 |
| -8 |
| n |
| 1 |
| 2 |
| 8 |
| n |
|
∴CD最短为5,
此时
| 1 |
| 2 |
| 8 |
| n |
过点B作BE∥y轴交AD于点E,则B(2,-4),E(2,2),BE=6,
∴S四边形ABCD=S△ABE+S四边形BEDC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了反比例函数与一次函数的综合应用,利用数形结合将已知正确的运用于两种函数,以及将四边形分割后求四边形面积是这部分重点题型,同学们应正确的掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 问栏杆多少长时,所用拉力F最小?是多少?
问栏杆多少长时,所用拉力F最小?是多少? 阅读理解:对于任意正实数a,b,
阅读理解:对于任意正实数a,b,
 阅读理解:
阅读理解: