摘要:(2)在同一个坐标系中画出的图象向上平移两个单位后的图象,(3)直接写出平移后的图象的解析式.注:图中小正方形网格的边长为1.
网址:http://m.1010jiajiao.com/timu_id_762576[举报]
已知抛物线![]() 的图象向上平移m个单位(
的图象向上平移m个单位(![]() )得到的新抛物线过点(1,8).
)得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成![]() 的形式;
的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴![]() 上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数
上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数![]() y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在
y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在![]() ≤
≤![]() 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;
(3)设一次函数![]() ,问是否存在正整数
,问是否存在正整数![]() 使得(2)中函数的函数值
使得(2)中函数的函数值![]() 时,对应的x的值为
时,对应的x的值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成y2=a(x-h)2+k的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在-3<x≤-
时对应的函数值y的取值范围;
(3)设一次函数y3=nx+3(n≠0),问是否存在正整数n使得(2)中函 数的函数值y=y3时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.
查看习题详情和答案>>
数的函数值y=y3时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.
查看习题详情和答案>>
(1)求m的值,并将平移后的抛物线解析式写成y2=a(x-h)2+k的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在-3<x≤-
| 3 | 2 |
(3)设一次函数y3=nx+3(n≠0),问是否存在正整数n使得(2)中函
 数的函数值y=y3时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.
查看习题详情和答案>>
数的函数值y=y3时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.
查看习题详情和答案>>
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成y2=a(x﹣h)2+k的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在﹣3<x≤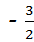 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;
(3)设一次函数y3=nx+3(n≠0),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由. 查看习题详情和答案>>
查看习题详情和答案>>
(1)求m的值,并将平移后的抛物线解析式写成y2=a(x﹣h)2+k的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在﹣3<x≤
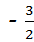 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;(3)设一次函数y3=nx+3(n≠0),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
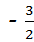 时对应的函数值y的取值范围;
时对应的函数值y的取值范围; ),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.
),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.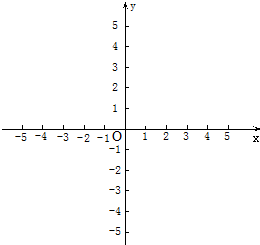
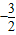 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;