(1)若和是等腰直角三角形.且.则是三角形．——青夏教育精英家教网——

摘要：(1)若和是等腰直角三角形.且.则是三角形．

网址：http://m.1010jiajiao.com/timu_id_762468[举报]

如图，平面直角坐标系中有一矩形纸片OABC，O为原点，点A，C分别在x轴，y轴上，点B坐标为（m，

）（其中m＞0），在BC边上选取适当的点E和点F，将△OCE沿OE翻折，得到△OGE；再将△ABF沿AF翻折，恰好使点B与点G重合，得到△AGF，且∠OGA=90度．

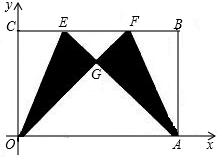（1）求m的值；
（2）求过点O，G，A的抛物线的解析式和对称轴；
（3）在抛物线的对称轴上是否存在点P，使得△OPG是等腰三角形？若不存在，请说明理由；若存在，直接答出所有满足条件的点P的坐标（不要求写出求解过程）．查看习题详情和答案>>

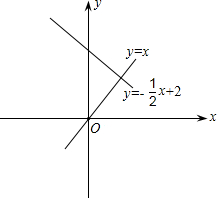如图，P是y轴上一动点，是否存在平行于y轴的直线x=t，使它与直线y=x和直线y=-

x+2分别交于点D、E（E在D的上方），且△PDE为等腰直角三角形？若存在，求t的值及点P的坐标；若不存在，请说明原因．查看习题详情和答案>>

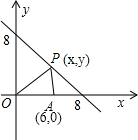如图，O是原点．点P（x，y）且x+y=8，点A的坐标为（6，0），设△OPA的面积为S．
（1）用含x的解析式表示S，写出x的取值范围．
（2）若点P在第一象限内，当点P所在的直线与X轴，Y轴分别相交于点B和C，且满足△BAP∽△CPO，求此时△OPA的面积．
（3）是否存在点P，使△OPA是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．查看习题详情和答案>>

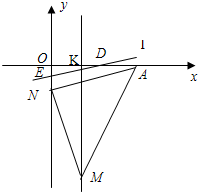18、如图，在平面直角坐标系中，点A（12，0），K（4，0）过点A的直线y=kx-4交y轴于点N．过K点且垂直于x轴的直线与过A点的直线y=2x+b交于点M．
（1）试判断△AMN的形状，并说明理由；
（2）将AN所在的直线l向上平移．平移后的直线l与x轴和y轴分别交于点D、E．当直线l平移时（包括l与直线AN重合），在直线MK上是否存在点P，使得△PDE是以DE为直角边的等腰直角三角形？若存在，直接写出所有满足条件的点P的坐标；若不存在，请说明理由．

查看习题详情和答案>>

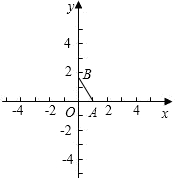如图，在平面直角坐标系中，已知点A（1，0）和点B（0，

），点C在坐标平面内．若以A，B，C为顶点构成的三角形是等腰三角形，且底角为30°，则满足条件的点C有

个．查看习题详情和答案>>