题目内容
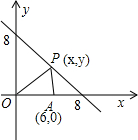 如图,O是原点.点P(x,y)且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
如图,O是原点.点P(x,y)且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.(1)用含x的解析式表示S,写出x的取值范围.
(2)若点P在第一象限内,当点P所在的直线与X轴,Y轴分别相交于点B和C,且满足△BAP∽△CPO,求此时△OPA的面积.
(3)是否存在点P,使△OPA是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)本题要分两种情况解答(当点P在第一、二象限内;当点P在第四象限内和x轴上时).
(2)过点P作PQ⊥X轴,交x轴于点Q,证明△BAP∽△CPO后利用线段比求出x的值,易求S△OAP.
(3)本题要分三种情况解答(OA=OP;PO=PA;AO=AP).
(2)过点P作PQ⊥X轴,交x轴于点Q,证明△BAP∽△CPO后利用线段比求出x的值,易求S△OAP.
(3)本题要分三种情况解答(OA=OP;PO=PA;AO=AP).
解答:解:(1)∵x+y=8,∴
y=-x+8,即y是x的一次函数,
∴它过的象限为一,二,四,
①当点P在第一、二象限内.
∵A和P点的坐标分别是(6,0)、(x,y),
∴S=3y.
∵x+y=8,∴y=8-x.
∴S=3(8-x)=24-3x.
∴所求的函数关系式为:S=-3x+24,(x<8);(1分)
②当点P在第四象限内和x轴上时.
S=
OA•|y|=-3y=-3(8-x)=-24+3x,(x≥8). (2分)
(2)过点P作PQ⊥X轴,交x轴于点Q.
∵∠OBC=45°,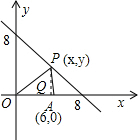
∴BP=
y.
∴CP=
(8-y)
∵△BAP∽△CPO,
∴
=
,
即
=
∴x=4±2
.
∴S△OAP=
=12±6
.
(3)①当OA=OP时,得点P1(2,6),P2(14,-6);
②当PO=PA时,得点P3(3,5);
③当AO=AP时得点P4(
+7,1-
),P5(-
+7,1+
). (5分)
y=-x+8,即y是x的一次函数,
∴它过的象限为一,二,四,
①当点P在第一、二象限内.
∵A和P点的坐标分别是(6,0)、(x,y),
∴S=3y.
∵x+y=8,∴y=8-x.
∴S=3(8-x)=24-3x.
∴所求的函数关系式为:S=-3x+24,(x<8);(1分)
②当点P在第四象限内和x轴上时.
S=
| 1 |
| 2 |
(2)过点P作PQ⊥X轴,交x轴于点Q.
∵∠OBC=45°,
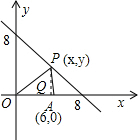
∴BP=
| 2 |
∴CP=
| 2 |
∵△BAP∽△CPO,
∴
| BA |
| CP |
| BP |
| CO |
即
| 2 | ||
|
| ||
| 8 |
∴x=4±2
| 2 |
∴S△OAP=
6×(4±2
| ||
| 2 |
| 2 |
(3)①当OA=OP时,得点P1(2,6),P2(14,-6);
②当PO=PA时,得点P3(3,5);
③当AO=AP时得点P4(
| 17 |
| 17 |
| 17 |
| 17 |
点评:本题考查的是相似三角形的判定以及一次函数的综合运用,考生要注意的是学会全面分析题目解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为点H.
为点H.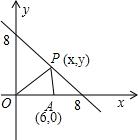 如图,O是原点.点P(x,y)且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
如图,O是原点.点P(x,y)且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
