摘要:(1)求点的个数,
网址:http://m.1010jiajiao.com/timu_id_760153[举报]
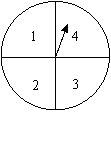
如图,把一个转盘分成四等份,依次标上数字1、2、3、4,若连续自由转动转盘二次,指针指向的数字分别记作![]() 把
把![]() 作为点
作为点![]() 的横、纵坐标.
的横、纵坐标.
(1)求点![]() 的个数;
的个数;
(2)求点![]() 在函数
在函数![]() 的图象上的概率.
的图象上的概率.
 |
查看习题详情和答案>>
如图,正方形ABCD和正方形EFGH的边长分别为2
和
,对角线BD、FH都在直线L上,O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距.当中心O2在直线L上平移时,正方形EFGH也随平移,在平移时正方形EFGH的形状、大小没有改变.
(1)计算:O1D= ,O2F= .
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2= .
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的 中心距的值或取值范围(不必写出计算过程).
查看习题详情和答案>>
中心距的值或取值范围(不必写出计算过程).
查看习题详情和答案>>
| 2 |
| 2 |
(1)计算:O1D=
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2=
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的
 中心距的值或取值范围(不必写出计算过程).
查看习题详情和答案>>
中心距的值或取值范围(不必写出计算过程).
查看习题详情和答案>>
 在一场篮球比赛中,一球星将球出手时,球离地面
在一场篮球比赛中,一球星将球出手时,球离地面| 20 |
| 9 |
(1)建立适当的平面直角坐标系,使得球出手时的坐标是(0,
| 20 |
| 9 |
(2)若球投入了离地面3米高的篮筐,请求篮筐离球星(坐标原点)的水平距离;
(3)如图,在篮球场地面以篮筐正下方点O为圆心一些同心的半圆弧,半圆弧上有一些投篮点,相邻的半圆之间宽度1 米,最内半圆弧的半径为r 米,其上每0.2π米的弧长上都是该球星投篮命中率较高的点(含半圆弧的两端点),其它半圆上的命中率较高的点个数与最内半圆弧上的个数相同,若该球星在(1)中投球站立的位置恰好在最外面的一个半圆弧上,求当r为多少时,投篮的同心半圆弧中投篮命中率较高的点的个数最多?
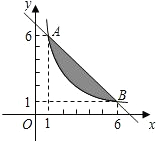 如图,A、B两点在函数y=
如图,A、B两点在函数y=| m | x |
(1)求m的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数. 查看习题详情和答案>>
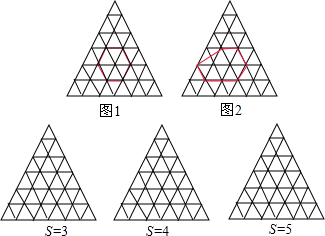 正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,设格点多边形各边上的格点的个数和为a,格点边多边形内部的格点个数和为b,格点多边形的面积为S,图l、图2是两个格点多边形.
正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,设格点多边形各边上的格点的个数和为a,格点边多边形内部的格点个数和为b,格点多边形的面积为S,图l、图2是两个格点多边形.(1)根据图中提供的信息填表:
| 一般格点多边形 | a | b | a+2b | S |
| 多边形1(图1) | 6 | 1 | ||
| 多边形2(图2) | 7 | 2 | 11 | |
| … | … | … | … | … |
(3)猜想S与a、b之间的关系:S=
(4)若一个格点多边形的面积为S,b是否存在最大值和最小值?若存在求出最大值和最小值;若不存在,请说明理由.