题目内容
 在一场篮球比赛中,一球星将球出手时,球离地面
在一场篮球比赛中,一球星将球出手时,球离地面| 20 |
| 9 |
(1)建立适当的平面直角坐标系,使得球出手时的坐标是(0,
| 20 |
| 9 |
(2)若球投入了离地面3米高的篮筐,请求篮筐离球星(坐标原点)的水平距离;
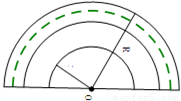
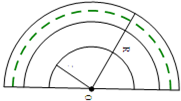
(3)如图,在篮球场地面以篮筐正下方点O为圆心一些同心的半圆弧,半圆弧上有一些投篮点,相邻的半圆之间宽度1 米,最内半圆弧的半径为r 米,其上每0.2π米的弧长上都是该球星投篮命中率较高的点(含半圆弧的两端点),其它半圆上的命中率较高的点个数与最内半圆弧上的个数相同,若该球星在(1)中投球站立的位置恰好在最外面的一个半圆弧上,求当r为多少时,投篮的同心半圆弧中投篮命中率较高的点的个数最多?
分析:(1)设抛物线顶点式解析式为y=a(x-4)2+4,然后利用待定系数法求二次函数解析式解答即可;
(2)令y=3,解关于x的一元二次方程,求出纵坐标是3的点的坐标,即可得到球星距离坐标原点的水平距离为7米;
(3)根据弧长公式求出最内半圆弧上的命中率较高的点的个数,再表示出到该球星所站的位置所在的最外面的弧线的条数,然后列式整理,再根据二次函数的最值问题解答即可.
(2)令y=3,解关于x的一元二次方程,求出纵坐标是3的点的坐标,即可得到球星距离坐标原点的水平距离为7米;
(3)根据弧长公式求出最内半圆弧上的命中率较高的点的个数,再表示出到该球星所站的位置所在的最外面的弧线的条数,然后列式整理,再根据二次函数的最值问题解答即可.
解答:解:(1)∵最高点坐标为(4,4),
∴设抛物线顶点式解析式为y=a(x-4)2+4,
∵球的出手点坐标为(0,
),
∴16a+4=
,
解得a=-
,
所以,函数关系式为y=-
(x-4)2+4;
(2)当y=3时,-
(x-4)2+4=3,
整理得,(x-4)2=9,
解得x1=1,x2=7,
∵球到达过最高点(4,4),
∴篮筐的坐标为(7,3),
∴篮筐距离球星的水平距离为7米;
(3)∵每0.2π米的弧长上都是该球星投篮命中率较高的点(含半圆弧的两端点),
∴最内半圆弧上的命中率较高的点的个数为:
+1=5r+1,
共有弧线条数为:7-r+1=8-r,
所以,投篮命中率较高的点的个数=(5r+1)(8-r)=-5r2+39r+8,
∵-
=-
=3.9,
∴半径r=4米时,投篮命中率较高的点的个数最多,
最大多的点数为:-5×42+39×4+8=84.
∴设抛物线顶点式解析式为y=a(x-4)2+4,
∵球的出手点坐标为(0,
| 20 |
| 9 |
∴16a+4=
| 20 |
| 9 |
解得a=-
| 1 |
| 9 |
所以,函数关系式为y=-
| 1 |
| 9 |
(2)当y=3时,-
| 1 |
| 9 |
整理得,(x-4)2=9,
解得x1=1,x2=7,
∵球到达过最高点(4,4),
∴篮筐的坐标为(7,3),
∴篮筐距离球星的水平距离为7米;
(3)∵每0.2π米的弧长上都是该球星投篮命中率较高的点(含半圆弧的两端点),
∴最内半圆弧上的命中率较高的点的个数为:
| πr |
| 0.2π |
共有弧线条数为:7-r+1=8-r,
所以,投篮命中率较高的点的个数=(5r+1)(8-r)=-5r2+39r+8,
∵-
| b |
| 2a |
| 39 |
| 2×(-5) |
∴半径r=4米时,投篮命中率较高的点的个数最多,
最大多的点数为:-5×42+39×4+8=84.
点评:本题考查了二次函数的应用,主要利用了待定系数法求二次函数解析式,已知函数值求自变量的值的方法,二次函数的最值问题,(3)确定出最内半圆弧上点的个数与弧线的条数是解题的关键,也是本题容易出错之处.

练习册系列答案
相关题目
 在一场篮球比赛中,一球星将球出手时,球离地面
在一场篮球比赛中,一球星将球出手时,球离地面 米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.
米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.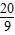 米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.
米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.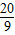 ),球运行的最高点坐标为(4,4),求出此坐标系中球的运行轨迹抛物线对应的函数关系式(不要求写取值范围);
),球运行的最高点坐标为(4,4),求出此坐标系中球的运行轨迹抛物线对应的函数关系式(不要求写取值范围);