摘要：2．用两种不同的方法计算
网址：http://m.1010jiajiao.com/timu_id_760083[举报]
作图题：
（1）如图：某通信公司要修建一座信号发射塔，要求发射塔到两城镇P、Q的距离相等，同时到两条高速公路l1、l2的距离也相等．在图上作出发射塔的位置．（不写作法，保留作图痕迹）
（2）由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）．请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑，使它成为轴对称图形．
（3）等边三角形给人以“稳如泰山”的美感，它具有独特的对称性．请你用三种不同的分割方法，将以下三个等边三角形分别分割成四个等腰三角形．（在图中画出分割线，并标出必要的角的度数）
查看习题详情和答案>>
（1）如图：某通信公司要修建一座信号发射塔，要求发射塔到两城镇P、Q的距离相等，同时到两条高速公路l1、l2的距离也相等．在图上作出发射塔的位置．（不写作法，保留作图痕迹）
（2）由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）．请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑，使它成为轴对称图形．
（3）等边三角形给人以“稳如泰山”的美感，它具有独特的对称性．请你用三种不同的分割方法，将以下三个等边三角形分别分割成四个等腰三角形．（在图中画出分割线，并标出必要的角的度数）
29、中央电视台每一期的“开心辞典”栏目，都有一个“二十四点”的趣味题，将四个数（四个数都用且只能用一次）进行“+”、“-”、“×”、“÷”运算，可加括号使其结果等于24．
例如：对1、2、3、4可作运算（1+2+3）×4=24，也可写成4×（1+2+3）=24，但视作相同方法的运算．
（1）现有四个有理数3，4，-6，10，请你用两种不同的算法计算出24，请分别写出算式；
（2）若给你四个有理数3，-5，7，-13，你还能凑出24吗？请写出一个算式．
查看习题详情和答案>>
例如：对1、2、3、4可作运算（1+2+3）×4=24，也可写成4×（1+2+3）=24，但视作相同方法的运算．
（1）现有四个有理数3，4，-6，10，请你用两种不同的算法计算出24，请分别写出算式；
（2）若给你四个有理数3，-5，7，-13，你还能凑出24吗？请写出一个算式．
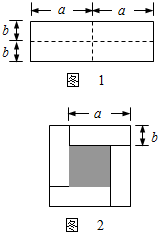如图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按如图2的形状拼成一个正方形．（1）图2的阴影部分的正方形的边长是
a-b
a-b
．（2）用两种不同的方法求图中阴影部分的面积．
【方法1】S阴影=
（a-b）2
（a-b）2
；【方法2】S阴影=
（a+b）2-4ab
（a+b）2-4ab
；（3）观察如图2，写出（a+b）2，（a-b）2，ab这三个代数式之间的等量关系．
（4）根据（3）题中的等量关系，解决问题：
若x+y=10，xy=16，求x-y的值．
将火柴盒ABCD推倒后，如图A所示，AB=CE，BC=EF，∠B=E=90°．
①连接AC、CF，并擦去AD、DC、GF，则得图B，根据图B说明：AC=CF；
②在①说明过程中，你还能得到哪些些结论，把它写下来，写满3个正确结论得2分，每多写一个正确结论加1分，不必说明理由；
③在图B中，请你连接AF，则四边形ACEF为梯形．设Rt△ABC的三边长如图所示，请你用两种不同的方法将梯形ABEF的面积S，用a、b、c表示出来；
④根据③的结论，你猜想Rt△ABC的三边长a、b、c之间有何数量关系？ 查看习题详情和答案>>
①连接AC、CF，并擦去AD、DC、GF，则得图B，根据图B说明：AC=CF；
②在①说明过程中，你还能得到哪些些结论，把它写下来，写满3个正确结论得2分，每多写一个正确结论加1分，不必说明理由；
③在图B中，请你连接AF，则四边形ACEF为梯形．设Rt△ABC的三边长如图所示，请你用两种不同的方法将梯形ABEF的面积S，用a、b、c表示出来；
④根据③的结论，你猜想Rt△ABC的三边长a、b、c之间有何数量关系？ 查看习题详情和答案>>
(本题6分)如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形.
【小题1】(1)图②中的阴影部分的正方形的边长等于_________________．
【小题2】(2)请用两种不同的方法列代数式表示图②中阴影部分的面积：
方法①_________________________________________________________．
方法②_________________________________________________________．
【小题3】(3)观察图②，写出(m＋n)2、(m－n)2、mn这三个代数式之间的等量关系．
【小题4】(4)根据(3)题中的等量关系，解决问题：已知a＋b＝6，ab＝4，求(a－b)2的值． 查看习题详情和答案>>
【小题1】(1)图②中的阴影部分的正方形的边长等于_________________．
【小题2】(2)请用两种不同的方法列代数式表示图②中阴影部分的面积：
方法①_________________________________________________________．
方法②_________________________________________________________．
【小题3】(3)观察图②，写出(m＋n)2、(m－n)2、mn这三个代数式之间的等量关系．
【小题4】(4)根据(3)题中的等量关系，解决问题：已知a＋b＝6，ab＝4，求(a－b)2的值． 查看习题详情和答案>>