��Ŀ����
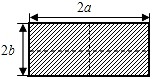
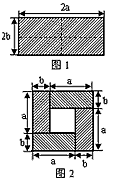
 ��ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ���������ֳ��Ŀ�С�����Σ�Ȼ����ͼ2����״ƴ��һ�������Σ�
��ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ���������ֳ��Ŀ�С�����Σ�Ȼ����ͼ2����״ƴ��һ�������Σ���1��ͼ2����Ӱ���ֵ������εı߳���
a-b
a-b
����2�������ֲ�ͬ�ķ�����ͼ����Ӱ���ֵ������
������1��S��Ӱ=
��a-b��2
��a-b��2
��������2��S��Ӱ=
��a+b��2-4ab
��a+b��2-4ab
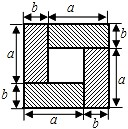
����3���۲���ͼ2��д����a+b��2����a-b��2��ab����������ʽ֮��ĵ�����ϵ��
��4�����ݣ�3�����еĵ�����ϵ��������⣺
��x+y=10��xy=16����x-y��ֵ��
��������1���۲�ͼ��ֱ�ӵó������εı߳���a-b��
��2�����ô������ε������ȥ4��С�����ε����������ֱ�����ã�1�����������С�����ε������
��3���ѣ�2���е���������ʽ�������ɣ�
��4����ȣ�3�������x-y��2���ٿ������ɣ�
��2�����ô������ε������ȥ4��С�����ε����������ֱ�����ã�1�����������С�����ε������
��3���ѣ�2���е���������ʽ�������ɣ�
��4����ȣ�3�������x-y��2���ٿ������ɣ�
����⣺��1��a-b��
��2������1��S��Ӱ=��a-b��2��
����2��S��Ӱ=��a+b��2-4ab��
��3����a-b��2=��a+b��2-4ab��
��4����x+y=10��xy=16��
�ࣨx-y��2=��x+y��2-4xy=102-4��14=36��
��x-y=��6��
��2������1��S��Ӱ=��a-b��2��
����2��S��Ӱ=��a+b��2-4ab��
��3����a-b��2=��a+b��2-4ab��
��4����x+y=10��xy=16��
�ࣨx-y��2=��x+y��2-4xy=102-4��14=36��
��x-y=��6��
�����������������ν�ϵ�˼�룬���о���ȫƽ��ʽ֮�����ϵ���Լ�����ʽ��ֵ�����⣬���ڻ������ͣ�

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ
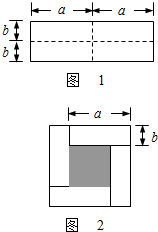
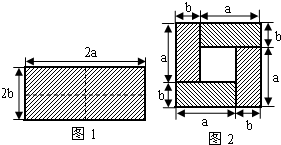 24����ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ�������ü������ȷֳ��Ŀ�С�����Σ�Ȼ��ͼ2��״ƴ��һ�������Σ�
24����ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ�������ü������ȷֳ��Ŀ�С�����Σ�Ȼ��ͼ2��״ƴ��һ�������Σ�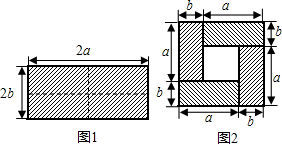 �Ŀ�С�����Σ�Ȼ��ͼ2��״ƴ��һ�������Σ�
�Ŀ�С�����Σ�Ȼ��ͼ2��״ƴ��һ�������Σ�