网址:http://m.1010jiajiao.com/timu_id_759499[举报]
[问题情境] 勾股定理是一条古老的数学定理,它有很多证明方法,我国汉代数学家赵爽根据弦图利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。
[定理表述] 请你根据图(1)中的直角三角形叙述勾股定理(用文字及符号语言叙述);

[尝试证明] 以图(1)中的直角三角形为基础可以构造出以a、b为底,以a+b为高的直角梯形如图(2)。请你利用图(2)验证勾股定理;
[知识拓展] 利用图(2)的直角梯形,我们可以证明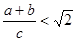 ,其证明步骤如下:
,其证明步骤如下:
∵BC=a+b,AD= .
又∵在直角梯形ABCD中有直角腰BC 斜腰AD(填“>”,“<”或“=”),即 。
∴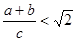
[问题情境] 勾股定理是一条古老的数学定理,它有很多证明方法,我国汉代数学家赵爽根据弦图利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。
[定理表述] 请你根据图(1)中的直角三角形叙述勾股定理(用文字及符号语言叙述);
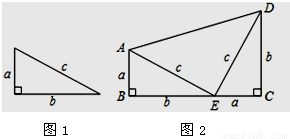
[尝试证明] 以图(1)中的直角三角形为基础可以构造出以a、b为底,以a+b为高的直角梯形如图(2)。请你利用图(2)验证勾股定理;
[知识拓展] 利用图(2)的直角梯形,我们可以证明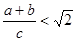 ,其证明步骤如下:
,其证明步骤如下:
∵BC=a+b,AD= .
又∵在直角梯形ABCD中有直角腰BC 斜腰AD(填“>”,“<”或“=”),即 。
∴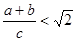
查看习题详情和答案>>
(1)如图①是一个重要公式的几何解释,请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,并且B、C、D三点共线,试证明∠ACE=90°;

(3)伽菲尔德(Garfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理。现请同学们沿着总统的思路,利用图②的面积表示验证勾股定理,请写出验证过程。
查看习题详情和答案>>请你根据图1中的直角三角形叙述勾股定理(分别用文字语言及符号语言叙述);
[尝试证明]
它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明.现以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;
[知识拓展]
如图3所示,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,已知A、B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
方案一:如图4所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图5所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.①在方案一中,a1=
②在方案二中,a2=
| x2+48 |
| x2+48 |
③请你分析:要使铺设的输气管道较短,应选择方案一还是方案二.

 如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在下面虚框中画出图形,并根据图形回答(2a+b)(a+2b)=
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.
①你画的图中需要C类卡片

②可将多项式a2+5ab+6b2分解因式为

(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式
A.xy=
| m2-n2 |
| 4 |
| m2+n2 |
| 2 |