网址:http://m.1010jiajiao.com/timu_id_75228[举报]
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
B
B
C
D
C
A
C
D
A
二、填空题:
13. 试题.files/image175.gif) 14.
14. 试题.files/image177.gif) 15. 2个 16.
15. 2个 16. 试题.files/image179.gif)
试题.files/image181.gif)
三、解答题:
17.解:(1)试题.files/image183.gif)
试题.files/image185.gif) ……………………3分
……………………3分
又 试题.files/image187.gif)
试题.files/image189.gif) 即
即 试题.files/image191.gif)
试题.files/image193.gif)
试题.files/image195.gif) …………………5分
…………………5分
(2)试题.files/image197.gif)
试题.files/image199.gif)
又 试题.files/image201.gif)
试题.files/image203.gif) 是
是试题.files/image205.gif) 的充分条件
的充分条件 试题.files/image207.gif) 解得
解得 试题.files/image209.gif) ………12分
………12分
18.由题意知,在甲盒中放一球概率为试题.files/image022.gif) 时,在乙盒中放一球的概率为
时,在乙盒中放一球的概率为试题.files/image212.gif) …2分
…2分
①当试题.files/image214.gif) 时,
时,试题.files/image216.gif) ,
,试题.files/image218.gif) 的概率为
的概率为试题.files/image220.gif) ………4分
………4分
②当试题.files/image222.gif) 时,
时,试题.files/image224.gif) ,又
,又试题.files/image226.gif) ,所以
,所以试题.files/image132.gif) 的可能取值为0,2,4
的可能取值为0,2,4
(?)当试题.files/image229.gif) 时,有
时,有试题.files/image231.gif) ,
,试题.files/image233.gif) ,它的概率为
,它的概率为试题.files/image235.gif) ………6分
………6分
(?)当试题.files/image237.gif) 时,有
时,有试题.files/image216.gif) ,
,试题.files/image240.gif) 或
或试题.files/image242.gif) ,
,试题.files/image244.gif)
它的概率为试题.files/image246.gif)
(?)当试题.files/image248.gif) 时,有
时,有试题.files/image250.gif) 或
或试题.files/image252.gif)
它的概率为试题.files/image254.gif)
故试题.files/image132.gif) 的分布列为
的分布列为
试题.files/image132.gif)
0
2
4
P
试题.files/image258.gif)
试题.files/image260.gif)
试题.files/image262.gif)
试题.files/image264.gif) 的数学期望
的数学期望试题.files/image266.gif) …………12分
…………12分
19.解:(1) 连接试题.files/image268.gif) 交
交试题.files/image270.gif) 于点E,连接DE,
于点E,连接DE,试题.files/image272.gif) ,
,
试题.files/image274.gif) 四边形
四边形试题.files/image276.gif) 为矩形,
为矩形,试题.files/image274.gif) 点E为
点E为试题.files/image268.gif) 的中点,
的中点,
试题.files/image274.gif)
试题.files/image281.gif)
试题.files/image274.gif)
试题.files/image284.gif) 平面
平面试题.files/image286.gif) ……………6分
……………6分
(2)作试题.files/image288.gif) 于F,连接EF
于F,连接EF
试题.files/image290.gif) ,D为AB中点,
,D为AB中点,试题.files/image292.gif) ,
,试题.files/image294.gif)
试题.files/image296.gif)
试题.files/image298.gif) ,
, 试题.files/image274.gif) EF为BE在平面
EF为BE在平面试题.files/image301.gif) 内的射影
内的射影
又试题.files/image303.gif) 为二面角
为二面角试题.files/image305.gif) 的平面角.
的平面角.
设试题.files/image307.gif)
试题.files/image309.gif)
试题.files/image311.gif)
又试题.files/image313.gif) 二面角
二面角试题.files/image305.gif) 的余弦值
的余弦值试题.files/image316.gif) ………12分
………12分
20.(1)据题意的
试题.files/image318.gif) ………4分
………4分
试题.files/image320.gif) ………5分
………5分
(2)由(1)得:当试题.files/image322.gif) 时,
时,试题.files/image324.gif)
试题.files/image326.gif)
当试题.files/image328.gif) 时,
时,试题.files/image330.gif) ,
,试题.files/image332.gif) 为增函数
为增函数
当试题.files/image334.gif) 时,
时,试题.files/image336.gif) 为减函数
为减函数
试题.files/image274.gif) 当
当试题.files/image339.gif) 时,
时,试题.files/image341.gif) …………………………8分
…………………………8分
当试题.files/image343.gif) 时,
时,试题.files/image345.gif)
当试题.files/image347.gif) 时,
时,试题.files/image349.gif)
当试题.files/image351.gif) 时,
时,试题.files/image353.gif) …………………………10分
…………………………10分
综上知:当试题.files/image339.gif) 时,总利润最大,最大值为195 ………………12分
时,总利润最大,最大值为195 ………………12分
21.解:(1)由椭圆定义可得试题.files/image356.gif) ,由
,由试题.files/image358.gif) 可得
可得
试题.files/image360.gif) ,而
,而试题.files/image362.gif)
解得 试题.files/image364.gif) ……………………4分
……………………4分
(2)由试题.files/image366.gif) ,得
,得试题.files/image368.gif) ,
,
试题.files/image370.gif)
解得试题.files/image372.gif) 或
或试题.files/image374.gif) (舍去)
(舍去) 试题.files/image376.gif) 此时
此时试题.files/image378.gif)
当且仅当试题.files/image380.gif) 时,
时,试题.files/image382.gif) 得最小值
得最小值试题.files/image384.gif) ,
,
此时椭圆方程为试题.files/image386.gif) ………………………………………8分
………………………………………8分
(3)由试题.files/image160.gif) 知点Q是AB的中点
知点Q是AB的中点
设A,B两点的坐标分别为试题.files/image389.gif) ,中点Q的坐标为
,中点Q的坐标为试题.files/image391.gif)
则试题.files/image393.gif) ,两式相减得
,两式相减得试题.files/image395.gif)
试题.files/image397.gif)
试题.files/image274.gif) AB的中点Q的轨迹为直线
AB的中点Q的轨迹为直线试题.files/image400.gif) ①
①
且在椭圆内的部分
又由试题.files/image162.gif) 可知
可知试题.files/image403.gif) ,所以直线NQ的斜率为
,所以直线NQ的斜率为试题.files/image405.gif) ,
,
方程为试题.files/image407.gif) ②
②
①②两式联立可求得点Q的坐标为试题.files/image409.gif)
试题.files/image201.gif) 点Q必在椭圆内
点Q必在椭圆内 试题.files/image412.gif) 解得
解得试题.files/image414.gif)
又试题.files/image416.gif)
试题.files/image418.gif) …………………………………12分
…………………………………12分
22.解:(1)由试题.files/image420.gif) ,得
,得试题.files/image422.gif)
令试题.files/image424.gif) ,有
,有试题.files/image426.gif)
试题.files/image428.gif)
试题.files/image430.gif)
又试题.files/image432.gif)
试题.files/image434.gif)
试题.files/image436.gif)
(2)证明:试题.files/image438.gif)
试题.files/image440.gif)
试题.files/image442.gif) 为递减数列
为递减数列
当试题.files/image444.gif) 时,
时,试题.files/image014.gif) 取最大值
取最大值
试题.files/image447.gif)
由(1)中知试题.files/image449.gif)
试题.files/image451.gif)
综上可知试题.files/image167.gif)
(3)试题.files/image454.gif)
欲证:试题.files/image173.gif) 即证
即证试题.files/image457.gif)
即试题.files/image459.gif) ,构造函数
,构造函数试题.files/image461.gif)
试题.files/image463.gif) 当
当试题.files/image465.gif) 时,
时,试题.files/image467.gif)
试题.files/image274.gif) 函数
函数试题.files/image332.gif) 在
在试题.files/image471.gif) 内递减
内递减
试题.files/image473.gif) 在
在试题.files/image475.gif) 内的最大值为
内的最大值为试题.files/image477.gif)
试题.files/image274.gif) 当
当试题.files/image106.gif) 时,
时,试题.files/image481.gif)
又试题.files/image483.gif)
试题.files/image485.gif)
试题.files/image274.gif) 不等式
不等式试题.files/image173.gif) 成立
成立
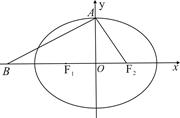
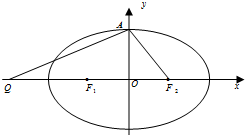 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
(1)求椭圆C的离心率;
(2)若过A、Q、F2三点的圆恰好与直线l:x-
| 3 |
(3)在(2)的条件下,过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形,如果存在,求出m的取值范围,如果不存在,说明理由.
. 查看习题详情和答案>>
 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
(1)若过A.Q.F2三点的圆恰好与直线l:x-
| 3 |
(2)在(1)的条件下,过右焦点F2作斜率为k的直线l与椭圆C交于M.N两点.试证明:
| 1 |
| |F2M| |
| 1 |
| |F2N| |
(1)求实数m的取值范围;
(2)在直线l:y=x+2上存在一点E,使得?|EF1|+|EF2|取得最小值,求此最小值及此时椭圆的方程;
(3)在条件(2)下的椭圆方程,是否存在斜率为k(k≠0)的直线l与椭圆交于不同的两点A、B,满足![]() =
=![]() ,且使得过点N(0,-1)、Q的直线,有
,且使得过点N(0,-1)、Q的直线,有![]() ·
·![]() =0?若存在,求出k的取值范围,若不存在,说明理由.
=0?若存在,求出k的取值范围,若不存在,说明理由.
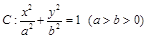 的左、右焦点分别为
的左、右焦点分别为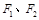 ,上顶点为
,上顶点为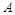 ,离心率为
,离心率为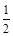 ,
在
,
在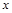 轴负半轴上有一点
轴负半轴上有一点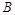 ,且
,且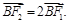
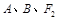 三点的圆 恰好与直线
三点的圆 恰好与直线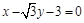 相切,求椭圆C的方程;
相切,求椭圆C的方程;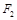 作斜率为
作斜率为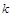 的直线
的直线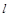 与椭圆C交于
与椭圆C交于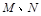 两点,在
两点,在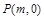 ,使得以
,使得以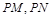 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出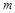 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.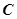 :
: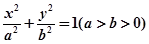 的左、右焦点分别为
的左、右焦点分别为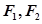 ,上顶点为
,上顶点为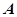 ,过点
,过点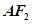 垂直的直线交
垂直的直线交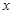 轴负半轴于点
轴负半轴于点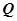 ,且
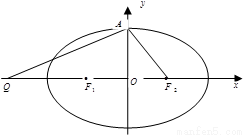
,且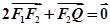 .
.
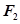 三点的圆恰好与直线
三点的圆恰好与直线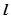 :
: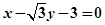 相切,求椭圆
相切,求椭圆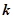 的直线
的直线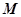 、
、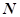 两点,在
两点,在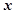 轴上是否存在点
轴上是否存在点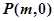 使得以
使得以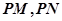 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出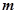 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.