摘要:.E.试在直线上确定一点Q.使点Q到D.E两点的距离之和最小.并求出Q点坐标.
网址:http://m.1010jiajiao.com/timu_id_750317[举报]
已知:如图,点I在x轴上,以I为圆心、r为半径的半圆I与x轴相交于点A、B,与y轴相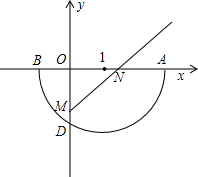 交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
(1)证明:无论半径r取何值时,点P都在某一个正比例函数的图象上.
(2)已知两点M(0,-1)、N(1、0),且射线MN与抛物线y=ax2+bx+c有两个不同的交点,请确定r的取值范围.
(3)请简要描述符合本题所有条件的抛物线的特征. 查看习题详情和答案>>
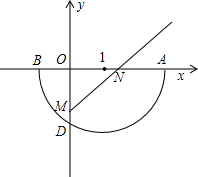 交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.(1)证明:无论半径r取何值时,点P都在某一个正比例函数的图象上.
(2)已知两点M(0,-1)、N(1、0),且射线MN与抛物线y=ax2+bx+c有两个不同的交点,请确定r的取值范围.
(3)请简要描述符合本题所有条件的抛物线的特征. 查看习题详情和答案>>
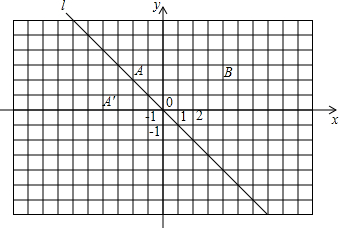
如图,在平面直角坐标系xOy中,函数y=-x的图象l是第二、四象限的角平分线.实验与探究:由图观察易知A(-1,3)关于直线l的对称点A′的坐标为(-3,1),请你写出点B(5,3)关于直线l的对称点B′的坐标:
归纳与发现:
结合图形,自己选点再试一试,通过观察点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标为
运用与拓广:
已知两点C(6,0),D(2,4),试在直线l上确定一点,使这点到C,D两点的距离之和最小,在图中画出这点的位置,保留作图痕迹,并求出这点的坐标.
查看习题详情和答案>>
(-3,-5)
(-3,-5)
;归纳与发现:
结合图形,自己选点再试一试,通过观察点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标为
(-n,-m)
(-n,-m)
;运用与拓广:
已知两点C(6,0),D(2,4),试在直线l上确定一点,使这点到C,D两点的距离之和最小,在图中画出这点的位置,保留作图痕迹,并求出这点的坐标.

如图,已知二次函数y=ax2+bx+c的图象经过三点A(-1,0),B(3,0),C(0,3),它的顶点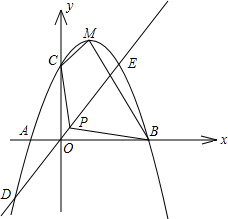 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
(1)求该二次函数的解析式,并求函数顶点M的坐标;
(2)已知点E(2,3),且二次函数的函数值大于正比例函数值时,试根据函数图象求出符合条件的自变量x的取值范围;
(3)当k为何值时且0<k<2,求四边形PCMB的面积为
.
(参考公式:已知两点D(x1,y1),E(x2,y2),则线段DE的中点坐标为(
,
))
查看习题详情和答案>>
 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.(1)求该二次函数的解析式,并求函数顶点M的坐标;
(2)已知点E(2,3),且二次函数的函数值大于正比例函数值时,试根据函数图象求出符合条件的自变量x的取值范围;
(3)当k为何值时且0<k<2,求四边形PCMB的面积为
| 93 |
| 16 |
(参考公式:已知两点D(x1,y1),E(x2,y2),则线段DE的中点坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
在直角坐标系中,已知两点A(-8,3)、B(-4,5)以及动点C(0,n)、D(m,0),则当四边形ABCD的周长最小时,比值
为( )
| m |
| n |
A、-
| ||
| B、-2 | ||
C、-
| ||
| D、-3 |