题目内容

阅读材料：

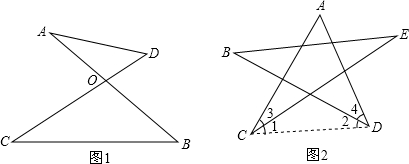
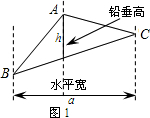
    如图(1)，在四边形ABCD中，对角线AC⊥BD，垂足为P，求证：S四边形ABCD＝AC·BD．

    证明：∵AC⊥BD　　∴

    ∴S四边形ABCD＝S△ACD＋S△ABC＝AC·PD＋AC·PB＝AC(PD＋PB)＝AC ·BD

解答问题：

(1)上述证明得到的性质可叙述为：    ▲   

(2)已知：如图(2)，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD＝3cm，BC＝7cm，利用上述的性质求梯形的面积．

练习册系列答案
相关题目
25、阅读材料：
如图（一），在已建立直角坐标系的方格纸中，图形①的顶点为A、B、C，要将它变换到图④（变换过程中图形的顶点必须在格点上，且不能超出方格纸的边界）．
例如：将图形①作如下变换（如图二）．
第一步：平移，使点C（6，6）移至点（4，3），得图②；
第二步：旋转，绕着点（4，3）旋转180°，得图③；
第三步：平移，使点（4，3）移至点O（0，0），得图④．
则图形①被变换到了图④．

解决问题：
（1）在上述变化过程中A点的坐标依次为：
（4，6）→（
2
，
3
）→（
6
，
3
）→（
2
，
0
）
（2）如图（三），仿照例题格式，在直角坐标系的方格纸中将△DEF经过平移、旋转、翻折等变换得到△OPQ．（写出变换步骤，并画出相应的图形）
精英家教网阅读材料：
如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：S△ABC=
12
ah，即三角形面积等于水平宽与铅垂高乘积的一半．
解答下列问题：精英家教网
如图2，抛物线顶点坐标为点C（-1，-4），交x轴于点A（-3，0），交y轴于点B．
（1）求抛物线和直线AB的解析式；
（2）点P是抛物线（在第三象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；
（3）是否存在一点P，使S△PAB=S△CAB，若存在，求出P点的坐标；若不存在，请说明理由．
（2013•益阳）阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x1，y1），B（x2，y2），AB中点P的坐标为（xp，yp）．由xp-x1=x2-xp，得xp=
x1+x2
2
，同理yp=
y1+y2
2
，所以AB的中点坐标为(
x1+x2
2
，
y1+y2
2
)．由勾股定理得AB2=
.
x2-x1
  
.
2+
.
y2-y1
  
.
2，所以A、B两点间的距离公式为AB=
(x2-x1)2+(y2-y1)2
．
注：上述公式对A、B在平面直角坐标系中其它位置也成立．
解答下列问题：
如图2，直线l：y=2x+2与抛物线y=2x2交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．
（1）求A、B两点的坐标及C点的坐标；
（2）连结AB、AC，求证△ABC为直角三角形；
（3）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．
阅读材料：如图，AB=AC，BD=CD，则可证得AD平分∠BAC，据此我们引出了“角平分线”的尺规作法．

问题：如图，AD=AE，AB=AC，也可证得AP平分∠BAC，据此我们能否引出了“角平分线”的第二种尺规作法呢？请在图中尝试着画出∠α的平分线．
阅读材料：

如图1，AB、CD交于点O，我们把△AOD和△BOC叫做对顶三角形．
结论：若△AOD和△BOC是对顶三角形，则∠A+∠D=∠B+∠C．
结论应用举例：
如图2：求五角星的五个内角之和，即∠A+∠B+∠ACE+∠ADB+∠E的度数．
解：连接CD，由对顶三角形的性质得：∠B+∠E=∠1+∠2，
在△ACD中，∵∠A+∠ACD+∠ADC=180°，
即∠A+∠3+∠1+∠2+∠4=180°，
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°．
解决问题：
（1）如图①，∠A+∠B+∠C+∠D+∠E+∠F=
360°
360°
；
（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F+∠G=
540°
540°
；
（3）如图③，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
720°
720°
；
（4）如图④，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=
1080°
1080°
；
请你从图③或图④中任选一个，写出你的计算过程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网