题目内容
如图(1),由直角三角形边角关系,可将三角形面积公式变形,
即: 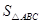 =
=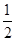 AB·CD,
AB·CD,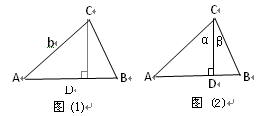
在Rt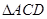 中,
中,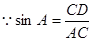 ,
,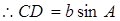
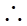
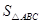 =
=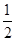 bc·sin∠A.
bc·sin∠A.
即 三角形的面积等于两边之长与夹角正弦之积的一半.
如图(2),在 ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ 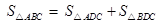 , 由公式①,得
, 由公式①,得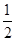 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 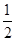 AC·CD·sinα+
AC·CD·sinα+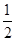 BC·CD·sinβ,
BC·CD·sinβ,
即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ
请你利用直角三角形边角关系,消去②中的AC、BC、CD,只用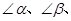
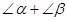 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).
【小题1】(1)______________________________________________________________
【小题2】(2)利用这个结果计算: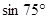 =_________________________
=_________________________
【小题1】(1) sin(α+β)=sinα•cosβ+cosα•sinβ
【小题2】(2) 
解析

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
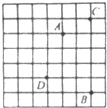 15、如图,大正方形是由49个边长为l的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,由其中三个点为顶点的直角三角形的个数是( )
15、如图,大正方形是由49个边长为l的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,由其中三个点为顶点的直角三角形的个数是( )