摘要：已知抛物线与轴相交于点..且是方程的两个实数根.点为抛物线与轴的交点．
网址：http://m.1010jiajiao.com/timu_id_746384[举报]
已知：抛物线y=ax2+bx+c的对称轴为x=
且经过点C（0，-3）和点F（3，-2
）．
（1）求抛物线的解析式：
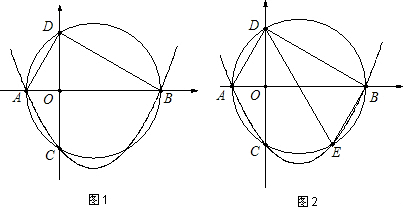
（2）如图1，设抛物线y=ax2+bx+c与x 轴交于A、B两点，与y 轴交于点C，过A、B、C三点的⊙M交y 轴于另一点D，连接AD、DB，设∠CDB=α，∠ADC=β，求cos（α-β）的值；
（3）如图2，作∠CDB的平分线DE交⊙M于点E，连接BE，问：在坐标轴上是否存在点P，使得以P、D、E为顶点的三角形与△DEB相似．若存在，求出所有满足条件的点P的坐标（不包括点B）；若不存在，请说明理由．
查看习题详情和答案>>
| 3 |
| 3 |
（1）求抛物线的解析式：
（2）如图1，设抛物线y=ax2+bx+c与x 轴交于A、B两点，与y 轴交于点C，过A、B、C三点的⊙M交y 轴于另一点D，连接AD、DB，设∠CDB=α，∠ADC=β，求cos（α-β）的值；
（3）如图2，作∠CDB的平分线DE交⊙M于点E，连接BE，问：在坐标轴上是否存在点P，使得以P、D、E为顶点的三角形与△DEB相似．若存在，求出所有满足条件的点P的坐标（不包括点B）；若不存在，请说明理由．
查看习题详情和答案>>
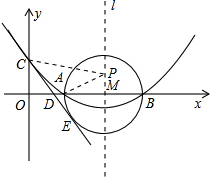（2013•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，-| 2 | 3 |
（1）求抛物线的解析式及A，B两点的坐标；
（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在，求AP+CP的最小值，若不存在，请说明理由；
（3）以AB为直径的⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．
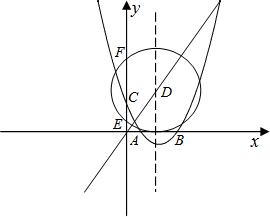
如图，在平面直角坐标系中，已知抛物线与x轴交于A（2，0），B（6，0）两点，交y轴于C（0，2
）．
（1）求抛物线的解析式；
（2）若此抛物线的对称轴与直线y=2x交于点D，作⊙D与x轴相切，⊙D交y轴于点E、F两点，求劣弧EF的长；
（3）若点P是此抛物线上在第二象限图象上的一点，PG垂直于x轴，垂足为点G，试确定P点的位置，使得△PGA的面积被直线AC分为1：2两部分．
查看习题详情和答案>>
| 3 |
（1）求抛物线的解析式；
（2）若此抛物线的对称轴与直线y=2x交于点D，作⊙D与x轴相切，⊙D交y轴于点E、F两点，求劣弧EF的长；
（3）若点P是此抛物线上在第二象限图象上的一点，PG垂直于x轴，垂足为点G，试确定P点的位置，使得△PGA的面积被直线AC分为1：2两部分．
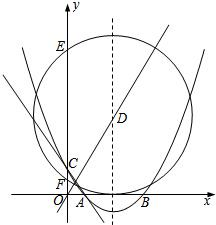6，0）两点，交y轴于点
与
轴相交于A、B两点，其对称轴为直线
，且与x轴交于点D，AO=1．
=_______。
=_______，点B的坐标为(_______，_______)：