摘要：11．如下图.已知点O是△ABC的∠ABC和∠ACB平分线的交点.过O作EF平行于BC交AB于E.交AC于F.AB=12.AC=18.则△AEF的周长是
网址：http://m.1010jiajiao.com/timu_id_743545[举报]
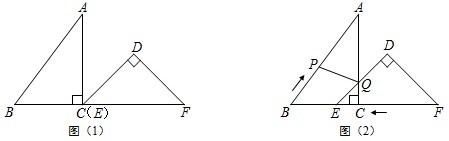
已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=9cm．
如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿BA向点A匀速移动．当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动、DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由；
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．
查看习题详情和答案>>
如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿BA向点A匀速移动．当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动、DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由；
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．
查看习题详情和答案>>
已知△ABC，
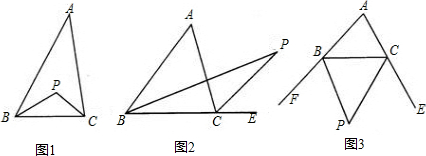
①如图1，若P点是∠ABC和∠ACB的角平分线的交点；
②如图2，若P点是∠ABC和∠ACE的角平分线的交点；
③如图3，若P点是∠CBF和∠BCE的角平分线的交点．
（1）探究上述三种情况下，∠P与∠A的数量关系（直接写出结论）；
（2）任选一种情况加以证明．
查看习题详情和答案>>
①如图1，若P点是∠ABC和∠ACB的角平分线的交点；
②如图2，若P点是∠ABC和∠ACE的角平分线的交点；
③如图3，若P点是∠CBF和∠BCE的角平分线的交点．
（1）探究上述三种情况下，∠P与∠A的数量关系（直接写出结论）；
（2）任选一种情况加以证明．
查看习题详情和答案>>
已知△ABC中，∠BAC=100°．
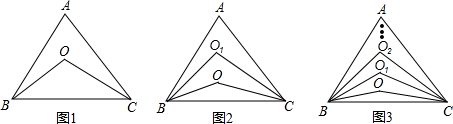
（1）若∠ABC和∠ACB的角平分线交于点O，如图1所示，试求∠BOC的大小；
（2）若∠ABC和∠ACB的三等分线（即将一个角平均分成三等分的射线）相交于O，O1，如图2所示，试求∠BOC的大小；
（3）如此类推，若∠ABC和∠ACB的n等分线自下而上依次相交于O，O1，O2…，如图3所示，试探求∠BOC的大小与n的关系，并判断当∠BOC=170°时，是几等分线的交线所成的角．
查看习题详情和答案>>
（1）若∠ABC和∠ACB的角平分线交于点O，如图1所示，试求∠BOC的大小；
（2）若∠ABC和∠ACB的三等分线（即将一个角平均分成三等分的射线）相交于O，O1，如图2所示，试求∠BOC的大小；
（3）如此类推，若∠ABC和∠ACB的n等分线自下而上依次相交于O，O1，O2…，如图3所示，试探求∠BOC的大小与n的关系，并判断当∠BOC=170°时，是几等分线的交线所成的角．
已知：如图1，在Rt△ABC中，∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ. 若设运动的时间为t(s)( 0＜t＜2 )，解答下列问题：
（1）t为何值时，PQ∥BC？
（2）设△AQP的面积为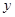
（
），求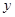与t之间的函数关系；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图2，连接PC，并把△PQC沿QC翻折，得到四边形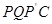
,那么是否存在t，使四边形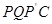为菱形？若存在，求出此时菱形的边长；若不存在，说明理由.
已知：如图1，在Rt△ABC中，∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ. 若设运动的时间为t(s)( 0＜t＜2 )，解答下列问题：
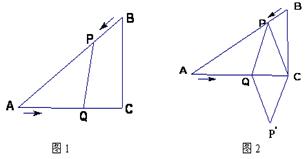
（1）t为何值时，PQ∥BC？
（2）设△AQP的面积为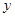
（
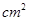），求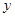与t之间的函数关系；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图2，连接PC，并把△PQC沿QC翻折，得到四边形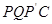
,那么是否存在t，使四边形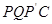为菱形？若存在，求出此时菱形的边长；若不存在，说明理由.
查看习题详情和答案>>