题目内容
已知△ABC,①如图1,若P点是∠ABC和∠ACB的角平分线的交点;
②如图2,若P点是∠ABC和∠ACE的角平分线的交点;
③如图3,若P点是∠CBF和∠BCE的角平分线的交点.
(1)探究上述三种情况下,∠P与∠A的数量关系(直接写出结论);
(2)任选一种情况加以证明.
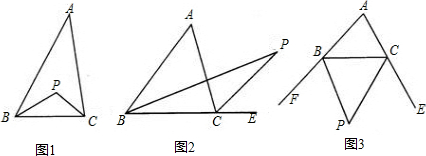
分析:根据三角形的外角性质、内角和定理、角平分线的定义探求并证明.
解答:解:(1)对于图1:∠P=90°+
∠A;
对于图2:∠P=
∠A;
对于图3:∠P=90°-
∠A;
(2)证明:如图2,∵BP平分∠ABC,CP平分∠ACE,
∴∠PBC=
∠ABC,∠ACP=
∠ACE.
又∵∠ACE是△ABC的外角,
∴∠ACE=∠A+∠ABC.
∵∠P=180°-∠PBC-∠BCP,
∴∠P=180°-
∠ABC-∠ACB-∠ACP
=180°-
∠ABC-∠ACB-
∠ACE
=180°-
(∠ABC+∠A+∠ABC)-∠ACB
=180°-∠ABC-
∠A-∠ACB
=180°-(∠ABC+∠ACB)-
∠A
=180°-(180°-∠A)-
∠A
=∠A-
∠A
=
∠A.
| 1 |
| 2 |
对于图2:∠P=
| 1 |
| 2 |
对于图3:∠P=90°-
| 1 |
| 2 |
(2)证明:如图2,∵BP平分∠ABC,CP平分∠ACE,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACE是△ABC的外角,
∴∠ACE=∠A+∠ABC.
∵∠P=180°-∠PBC-∠BCP,
∴∠P=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=180°-∠ABC-
| 1 |
| 2 |
=180°-(∠ABC+∠ACB)-
| 1 |
| 2 |
=180°-(180°-∠A)-
| 1 |
| 2 |
=∠A-
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查三角形外角的性质及三角形的内角和定理,是经常出现的题目,最好能记住.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
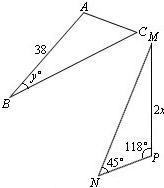 15、已知△ABC≌△PMN,如图,则x=
15、已知△ABC≌△PMN,如图,则x=

 ABC和
ABC和 ;
;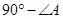 ;
;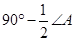 。
。
 ABC和
ABC和 ;
; ;
; 。
。