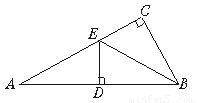
摘要：8．如左下图.在△ABC中.BC=8cm.AB的垂直平分线交AB于点D.交AC于点E.△BCE的周长等于18cm.则AC的长等于A.6 cm B.8 cm C.10 cm D.12 cm
网址：http://m.1010jiajiao.com/timu_id_741666[举报]
，DC=1，AC=
B.27 C.3 D.25
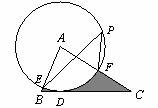
如下图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上一点，且∠EPF=40°，则图中阴影部分的面积是（ ）
A．
B．
C．
D．
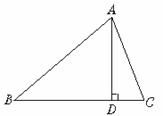
（1）如图1，在△ABC中，BC=3，AC=4，AB=5．D为AB边上一点，且△ACD与△BCD的周长相等，则AD=
（2）如图2，在△ABC中，BC=a，AC=b，AB2=BC2+AC2．E为BC边上一点，且△ABE与△ACE的周长相等；F为AC边上一点，且△ABF与△BCF的周长相等，求CE•CF（用含a，b的式子表示）．
查看习题详情和答案>>
2
2
．（2）如图2，在△ABC中，BC=a，AC=b，AB2=BC2+AC2．E为BC边上一点，且△ABE与△ACE的周长相等；F为AC边上一点，且△ABF与△BCF的周长相等，求CE•CF（用含a，b的式子表示）．
在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC2=AB2+BC2，BD2=AB2+AD2，又CD=AB，AD=BC，所以AC2+BD2=AB2+BC2+CD2+AD2=2（AB2+BC2）．
小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
（1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
（2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
（3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）
查看习题详情和答案>>
小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
（1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
（2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
（3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）
查看习题详情和答案>>