摘要：25．点A.B分别是两条平行线.上任意两点.在直线上找一点C.使.连结AC.在直线AC上任取一点E.作∠BEF=∠ABC.EF交直线于点F.
网址：http://m.1010jiajiao.com/timu_id_741038[举报]
5、试分别指出坐标平面内以下各直线上各点的横坐标、纵坐标的特征以及与两条坐标轴的位置关系．
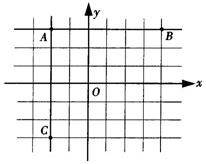
（1）在图中，过A（-2，3）、B（4，3）两点作直线AB，则直线AB上的任意一点P（a，b）的横坐标可以取
（2）在图中，过A（-2，3）、C（-2，-3）两点作直线AC，则直线AC上的任意一点Q（c，d）的横坐标是
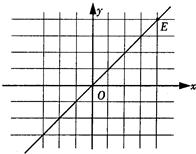
（3）在图中，过原点O和点E（4，4）两点作直线OE，我们发现，直线OE上的任意一点P（x，y）的横坐标与纵坐标
查看习题详情和答案>>
（1）在图中，过A（-2，3）、B（4，3）两点作直线AB，则直线AB上的任意一点P（a，b）的横坐标可以取
任意实数
，纵坐标是3
．直线AB与y轴垂直
，垂足的坐标是（0，3）
；直线AB与x轴平行
，AB与x轴的距离是3
．（2）在图中，过A（-2，3）、C（-2，-3）两点作直线AC，则直线AC上的任意一点Q（c，d）的横坐标是
-2
，纵坐标可以是任意实数
．直线AC与x轴垂直
，垂足的坐标是（-2，0）
；直线AC与y轴平行
，AC与y轴的距离是2
．（3）在图中，过原点O和点E（4，4）两点作直线OE，我们发现，直线OE上的任意一点P（x，y）的横坐标与纵坐标
相等
，并且直线OE平分
∠xOy．
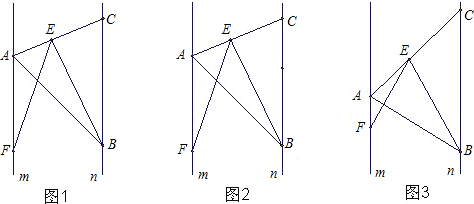
如图1，点A、B分别是两条平行线m、n上任意两点，在直线n上找一点C，使BC=kAB（k为常数），连接AC，在直线AC上任取一点E，作∠BEF=∠ABC，EF交直线m于点F．
（1）请说明∠AFE=∠ABE的理由；
（2）当k=1时，探究线段EF与EB的数量关系，并加以说明；
（3）当k≠1时，探究线段EF与EB的比值，请说明理由．
查看习题详情和答案>>
（1）请说明∠AFE=∠ABE的理由；
（2）当k=1时，探究线段EF与EB的数量关系，并加以说明；
（3）当k≠1时，探究线段EF与EB的比值，请说明理由．
查看习题详情和答案>>
如图1，点A、B分别是两条平行线m、n上任意两点，在直线n上找一点C，使BC=kAB（k为常数），连接AC，在直线AC上任取一点E，作∠BEF=∠ABC，EF交直线m于点F．
（1）请说明∠AFE=∠ABE的理由；
（2）当k=1时，探究线段EF与EB的数量关系，并加以说明；
（3）当k≠1时，探究线段EF与EB的比值，请说明理由．
查看习题详情和答案>>
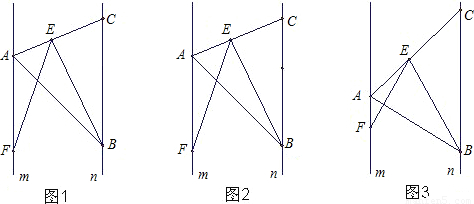
如图1，点A、B分别是两条平行线m、n上任意两点，在直线n上找一点C，使BC=kAB（k为常数），连接AC，在直线AC上任取一点E，作∠BEF=∠ABC，EF交直线m于点F．
（1）请说明∠AFE=∠ABE的理由；
（2）当k=1时，探究线段EF与EB的数量关系，并加以说明；
（3）当k≠1时，探究线段EF与EB的比值，请说明理由．
查看习题详情和答案>>
（1）请说明∠AFE=∠ABE的理由；
（2）当k=1时，探究线段EF与EB的数量关系，并加以说明；
（3）当k≠1时，探究线段EF与EB的比值，请说明理由．
查看习题详情和答案>>
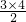=6条直线．请你仿照上面分析方法，回答下面问题：