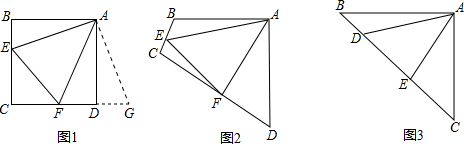
题目内容
如图1,点A、B分别是两条平行线m、n上任意两点,在直线n上找一点C,使BC=kAB(k为常数),连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.(1)请说明∠AFE=∠ABE的理由;
(2)当k=1时,探究线段EF与EB的数量关系,并加以说明;
(3)当k≠1时,探究线段EF与EB的比值,请说明理由.
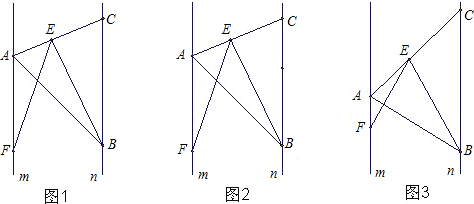
分析:(1)根据两直线平行,内错角相等求出∠FAB=∠ABC,∠BEF=∠ABC,所以可得到∠FAB=∠FEB,设AB、EF相交于点O,可以利用两角对应相等两三角形相似证明△AOF∽△EOB,然后根据相似三角形的对应角相等即可证明;
(2)过点E作ED⊥m,EP⊥AB,根据k=1可知AB=BC,再根据对边对等角的性质∠BAC=∠ACB,又两直线平行,内错角相等,可以证明AE平分∠DAP,所以ED=EP,然后证明△FDE与△EPB全等,根据全等三角形对应边相等即可证明;
(3)连接FB.设AB与EF交于点O,利用(1)的结论先证明△AOF∽△EOB,根据相似三角形对应边成比例得到
=
,再根据两边对应成比例,夹角相等证明△ACB∽△FBE,再根据相似三角形对应边成比例列出比例式即可得到线段EF、EB与线段AB、BC的关系.
(2)过点E作ED⊥m,EP⊥AB,根据k=1可知AB=BC,再根据对边对等角的性质∠BAC=∠ACB,又两直线平行,内错角相等,可以证明AE平分∠DAP,所以ED=EP,然后证明△FDE与△EPB全等,根据全等三角形对应边相等即可证明;
(3)连接FB.设AB与EF交于点O,利用(1)的结论先证明△AOF∽△EOB,根据相似三角形对应边成比例得到
| OA |
| OF |
| OE |
| OB |
解答: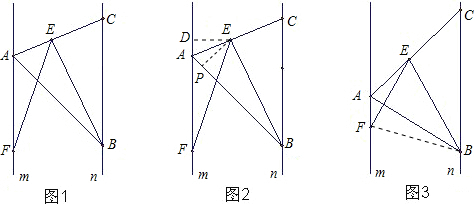 解:(1)∵m∥n,
解:(1)∵m∥n,
∴∠FAB=∠ABC,
∵∠FEB=∠ABC,
∴∠FAB=∠FEB,
∵∠AOF=∠EOB,
∴△AOF∽△EOB,
∴∠AFE=∠ABE;
(2)作ED⊥m,EP⊥AB,
∵k=1,
∴AB=BC,
∴∠BAC=∠ACB,
∵m∥n,
∴∠DAE=∠ACB,
∴∠DAE=∠BAC,
∴ED=EP(角平分线上的点到角的两边的距离相等),
在△FDE和△EPB中,
,
∴△FDE≌△EPB(AAS),
∴EF=EB(全等三角形对应边相等);
(3)连接FB,设AB与EF交于点O,
在△AOF和△EOB中,
,
∴△AOF∽△EOB,
∴
=
,
又∵∠AOE=∠FOB,
∴△AOE∽△FOB,
∴∠CAB=∠EFB,
∵∠FEB=∠ABC,
∴△ACB∽△FBE,
∴
=
=
.
 解:(1)∵m∥n,
解:(1)∵m∥n,∴∠FAB=∠ABC,
∵∠FEB=∠ABC,
∴∠FAB=∠FEB,
∵∠AOF=∠EOB,
∴△AOF∽△EOB,
∴∠AFE=∠ABE;
(2)作ED⊥m,EP⊥AB,
∵k=1,
∴AB=BC,
∴∠BAC=∠ACB,
∵m∥n,
∴∠DAE=∠ACB,
∴∠DAE=∠BAC,
∴ED=EP(角平分线上的点到角的两边的距离相等),
在△FDE和△EPB中,
|
∴△FDE≌△EPB(AAS),
∴EF=EB(全等三角形对应边相等);
(3)连接FB,设AB与EF交于点O,
在△AOF和△EOB中,
|
∴△AOF∽△EOB,
∴
| OA |
| OF |
| OE |
| OB |
又∵∠AOE=∠FOB,
∴△AOE∽△FOB,
∴∠CAB=∠EFB,
∵∠FEB=∠ABC,
∴△ACB∽△FBE,
∴
| EF |
| EB |
| AB |
| BC |
| 1 |
| k |
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,平行线的性质,综合性较强,对同学们的图形识别能力有较高的要求,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

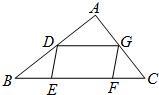 8、△ABC与平行四边形DEFG如图放置,点D,G分别在边AB,AC上,点E,F在边BC上.已知BE=DE,CF=FG,则∠A的度数( )
8、△ABC与平行四边形DEFG如图放置,点D,G分别在边AB,AC上,点E,F在边BC上.已知BE=DE,CF=FG,则∠A的度数( )