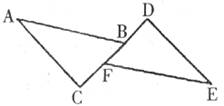
摘要:14.如下图.点B.F在CD上.∠C=∠D=90°.AB=EF.CF=BD.若∠A=35°.则∠DFE等于
网址:http://m.1010jiajiao.com/timu_id_740396[举报]
Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG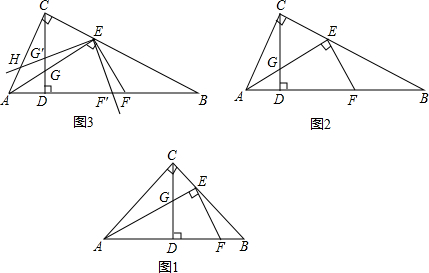
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3 ,且
,且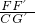 =
= ,求线段G′H的长.
,求线段G′H的长.
查看习题详情和答案>>
Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG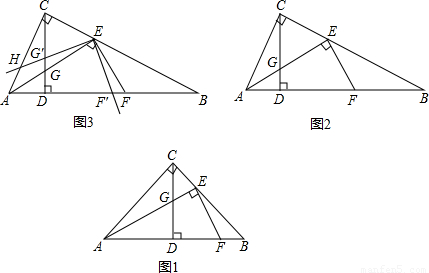
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3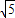 ,且
,且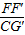 =
= ,求线段G′H的长.
,求线段G′H的长.
查看习题详情和答案>>
(1)如图1,当tan∠BAC=1时,求证:EF=2EG

(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3
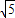 ,且
,且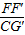 =
= ,求线段G′H的长.
,求线段G′H的长.查看习题详情和答案>>
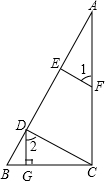 已知:如图,△ABC中,AC⊥BC,点D、E在AB边上,点F在AC边上,DG⊥BC于G,∠1=∠2.求证:EF∥CD.
已知:如图,△ABC中,AC⊥BC,点D、E在AB边上,点F在AC边上,DG⊥BC于G,∠1=∠2.求证:EF∥CD.
请将以下推理过程补充完整:
证明:∵DG⊥BC,AC⊥BC,( 已知 )
∴∠DGB=∠ACB=90°,( 垂直的定义 )
∴DG∥AC,(________)
∴∠2=________.(________)
∵∠1=∠2,( 已知 )
∴∠1=________,( 等量代换 )
∴EF∥CD.(________)
查看习题详情和答案>>
阅读与证明:
如图,已知正方形ABCD中,E、F分别是CD、BC上的点,且∠EAF=45 °,
求证:BF+DE=EF。
分析:证明一条线段等于另两条线段的和,常用“截长法”或“补短法”,将线段BF、DE放在同一直线上,构造出一条与BF+DE相等的线段。如图1延长ED至点F',使DF'=BF,连接A F',易证△ABF≌△ADF',进一步证明△AEF≌△AEF',即可得结论。
(1)请你将下面的证明过程补充完整。
证明:延长ED至F',使DF'=BF,
∵ 四边形ABCD是正方形
∴ AB=AD,∠ABF=∠ADF'=90°,
∴ △ABF≌△ADF'(SAS)
应用与拓展:如图建立平面直角坐标系,使顶点A与坐标原点O重合,边OB、OD分别在x轴、y轴的正半轴上。
(2)设正方形边长OB为30,当E为CD中点时,试问F为BC的几等分点?并求此时F点的坐标;
(3)设正方形边长OB为30,当EF最短时,直接写出直线EF的解析式: 。
如图,已知正方形ABCD中,E、F分别是CD、BC上的点,且∠EAF=45 °,
求证:BF+DE=EF。
分析:证明一条线段等于另两条线段的和,常用“截长法”或“补短法”,将线段BF、DE放在同一直线上,构造出一条与BF+DE相等的线段。如图1延长ED至点F',使DF'=BF,连接A F',易证△ABF≌△ADF',进一步证明△AEF≌△AEF',即可得结论。
(1)请你将下面的证明过程补充完整。
证明:延长ED至F',使DF'=BF,
∵ 四边形ABCD是正方形
∴ AB=AD,∠ABF=∠ADF'=90°,
∴ △ABF≌△ADF'(SAS)
应用与拓展:如图建立平面直角坐标系,使顶点A与坐标原点O重合,边OB、OD分别在x轴、y轴的正半轴上。
(2)设正方形边长OB为30,当E为CD中点时,试问F为BC的几等分点?并求此时F点的坐标;
(3)设正方形边长OB为30,当EF最短时,直接写出直线EF的解析式: 。