Question

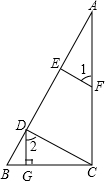已知：如图，△ABC中，AC⊥BC，点D、E在AB边上，点F在AC边上，DG⊥BC于G，∠1=∠2．求证：EF∥CD．
请将以下推理过程补充完整：
证明：∵DG⊥BC，AC⊥BC，（ 已知 ）
∴∠DGB=∠ACB=90°，（ 垂直的定义 ）
∴DG∥AC，（________）
∴∠2=________．（________）
∵∠1=∠2，（ 已知 ）
∴∠1=________，（ 等量代换 ）
∴EF∥CD．（________）

Answer 1

同位角相等，两直线平行    ∠∠DCA    两直线平行，内错角相等    ∠DCA    同位角相等，两直线平行
分析：首先证明∠2=∠DCA，然后根据∠1=∠2，可得∠DCA=∠1，再根据同位角相等，两直线平行可判定出EF∥DC．
解答：证明：∵DG⊥BC，AC⊥BC，（ 已知 ）
∴∠DGB=∠ACB=90°，（ 垂直的定义 ）
∴DG∥AC，（ 同位角相等，两直线平行）
∴∠2=∠DCA．（ 两直线平行，内错角相等）
∵∠1=∠2，（ 已知 ）
∴∠1=∠DCA，（ 等量代换 ）
∴EF∥CD．（ 同位角相等，两直线平行）
点评：此题主要考查了平行线的判定与性质定理，关键是掌握平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．