题目内容
Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG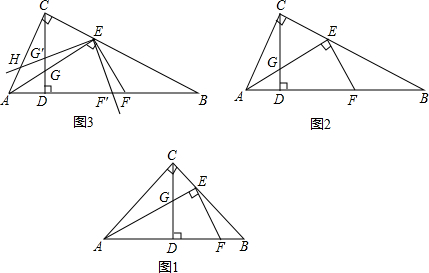
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
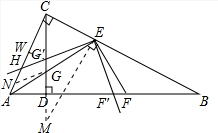
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3 ,且
,且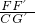 =
= ,求线段G′H的长.
,求线段G′H的长.
 (1)证明:在Rt△ABC中,tan∠BAC=1=tan45°,
(1)证明:在Rt△ABC中,tan∠BAC=1=tan45°,∴∠BAC=45°,
∵∠ACB=90°,
∴∠ABC=45°.
∴△ABC为等腰直角三角形,
∵CD⊥AB,
∴∠BCD=45°,
过E点作EK⊥BC,EK与CD相交于点K,
∴∠GKE=45°=∠B
∵∠GEK+∠KEF=90°=∠KEF+∠BEF,
∴∠GEK=∠FEB,
∴△GEK∽△FEB,
∴
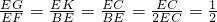 ,
,∴EF=2EG;
(2)根据(1)的证明,同理可证:
当tan∠BAC=2时,EF=EG;
(3)在Rt△ABC中,∠ACB=90°,CD⊥AB,
则tan∠BAC=tan∠CAD=tan∠BCD=2,
设AC=3k,则
 ,
,过点E作EM⊥BC,EM与CD的延长线相交于点M,tan∠ECM=2,
∴EM=4k.
在△AGC与△EGM中,
∵AC∥EM,
∴∠ACG=∠M.∠AGC=∠EGM,
∴△AGC∽△EGM
∴
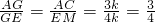
过点G作GN∥EH,与AH相交于点N,
∴△ANG∽△AHE,
∴
 =
= ,
,∴
 ,∴
,∴
∠GEM+∠MEF=90°=∠MEF+∠FEB,
∴∠GEM=∠FEB,
∠M=∠B,
∴△GEM∽△FEB,
∴
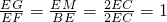 ,
,∴EF=EG.
同理可证EF′=EG′.∠FEF'=∠GEG',
∴△GEG'≌△FEF',
∴FF'=GG',
∴
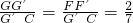 .
.HG′∥NG,同理可证
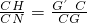 ,
,∴
 ,
,∴
 ,
,∴
 ,
,∴
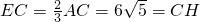
∴△HCE是等腰直角三角形,∠CHE=45°,
在△HG'C中,过点G'作G'W⊥CH,垂足是W,
设G'W=x,则
 ,
,∴CW=2x,CW+HW=CH,
∴
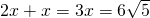 ,
,∴
 ,
,∴
 .
.分析:(1)根据tan∠BAC=1=tan45°,得出△ABC为等腰直角三角形,再过E点作EK⊥BC,EK与CD相交于点K,得出∠GKE=45°=∠B,再根据∠GEK+∠KEF=90°=∠KEF+∠BEF,得出△GEK∽△FEB,从而证出
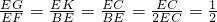 ,即可得出EF=2EG;
,即可得出EF=2EG;(2)根据(1)的证明过程,同理可证出当tan∠BAC=2时,得出EF=EG;
(3)根据(2)的结论,先设AC=3k,得出
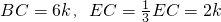 ,再过点E作EM⊥BC,EM与CD的延长线相交于点M,得出△AGC∽△EGM,得出
,再过点E作EM⊥BC,EM与CD的延长线相交于点M,得出△AGC∽△EGM,得出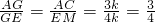 ,再过点G作GN∥EH,与AH相交于点N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可证EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可证出
,再过点G作GN∥EH,与AH相交于点N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可证EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可证出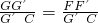 的值,再根据HG′∥NG,同理可证
的值,再根据HG′∥NG,同理可证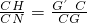 ,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,从而得出G′H 的值.
,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,从而得出G′H 的值.点评:此题考查了相似三角形的判定与性质;解决本题的关键是根据直角三角形的性质以及相似三角形的性质得到它们的比值进行计算即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
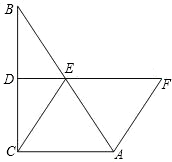 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=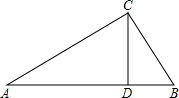 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=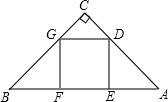 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为