摘要:14.关于.y的方程组的解是一对相同的数.则= .
网址:http://m.1010jiajiao.com/timu_id_737555[举报]
25、在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法、善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对相关知识进行了归纳整理.
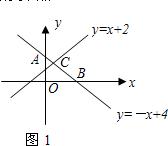
(1)例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图象(如图1),并作了归纳:
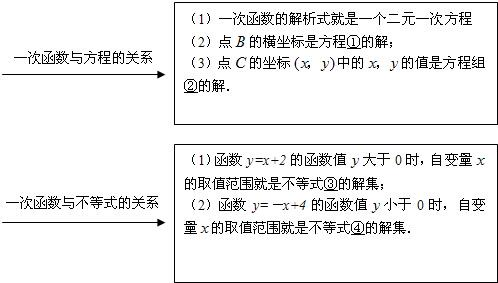
请根据图1和以上方框中的内容,在下面数字序号后写出相应的结论:
①
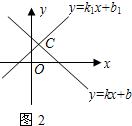
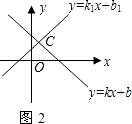
(2)若已知一次函数y=k1x+b1和y=kx+b的图象(如图2),且它们的交点C的坐标为(1,3),那么不等式kx+b≥k1x+b1的解集是
查看习题详情和答案>>


(1)例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图象(如图1),并作了归纳:

请根据图1和以上方框中的内容,在下面数字序号后写出相应的结论:
①
-x+4=0
;②x+2=0
;③x+2>0
;④-x+4<0
;(2)若已知一次函数y=k1x+b1和y=kx+b的图象(如图2),且它们的交点C的坐标为(1,3),那么不等式kx+b≥k1x+b1的解集是
x≤1
.在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法、善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对相关知识进行了归纳整理.
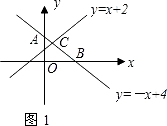
(1)例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图象(如图1),并作了归纳:
请根据图1和以上方框中的内容,在下面数字序号后写出相应的结论:
①______;②______;③______;④______;
(2)若已知一次函数y=k1x+b1和y=kx+b的图象(如图2),且它们的交点C的坐标为(1,3),那么不等式kx+b≥k1x+b1的解集是______.
查看习题详情和答案>>
(2013•鹰潭模拟)某校九年级(1)班数学兴趣小组开展了一次活动,过程如下:
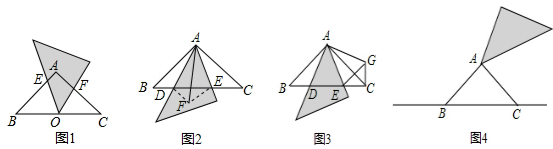
如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小明将一块直角三角板的直角顶点放在斜边BC边的中点O上,从BC边开始绕点A顺时针旋转,其中三角板两条直角边所在的直线分别交AB、AC于点E、F.
(1)小明在旋转中发现:在图1中,线段AE与CF相等.请你证明小明发现的结论;
(2)小明将一块三角板中含45°角的顶点放在点A上,从BC边开始绕点A顺时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.当0°<α≤45°时,小明在旋转中还发现线段BD、CE、DE之间存在如下等量关系:
BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决:
小颖的方法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2);
小亮的方法:将△ABD绕点A逆时针旋转90°得到△ACG,连接EG(如图3).
请你从中任选一种方法进行证明;
(3)小明继续旋转三角板,在探究中得出:当45°<α<135°且α≠90°时,等量关系BD2+CE2=DE2仍然成立.现请你继续探究:当135°<α<180°时(如图4),等量关系BD2+CE2=DE2是否仍然成立?若成立,给出证明;若不成立,说明理由.
查看习题详情和答案>>
如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小明将一块直角三角板的直角顶点放在斜边BC边的中点O上,从BC边开始绕点A顺时针旋转,其中三角板两条直角边所在的直线分别交AB、AC于点E、F.
(1)小明在旋转中发现:在图1中,线段AE与CF相等.请你证明小明发现的结论;
(2)小明将一块三角板中含45°角的顶点放在点A上,从BC边开始绕点A顺时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.当0°<α≤45°时,小明在旋转中还发现线段BD、CE、DE之间存在如下等量关系:
BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决:
小颖的方法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2);
小亮的方法:将△ABD绕点A逆时针旋转90°得到△ACG,连接EG(如图3).
请你从中任选一种方法进行证明;
(3)小明继续旋转三角板,在探究中得出:当45°<α<135°且α≠90°时,等量关系BD2+CE2=DE2仍然成立.现请你继续探究:当135°<α<180°时(如图4),等量关系BD2+CE2=DE2是否仍然成立?若成立,给出证明;若不成立,说明理由.
